Probability and Likelihood
Day 4
Freie Universität Berlin @ Theoretical Ecology
January 18, 2024
1 Reproduce slides
2 What concepts you will learn
- probability
- probability distributions:
- difference between discrete and continous distributions
- probability mass function (pmf), probability density function (pdf)
- cumulative distribution function (cdf)
- quantile function (inverse cdf)
- generating random numbers from a distribution
- how to fit statistical models/distributions to data: likelihood
3 Probability
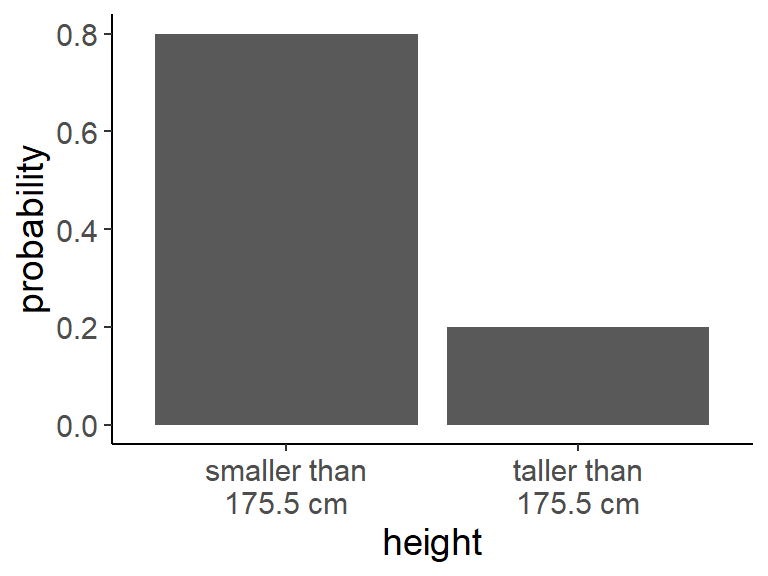
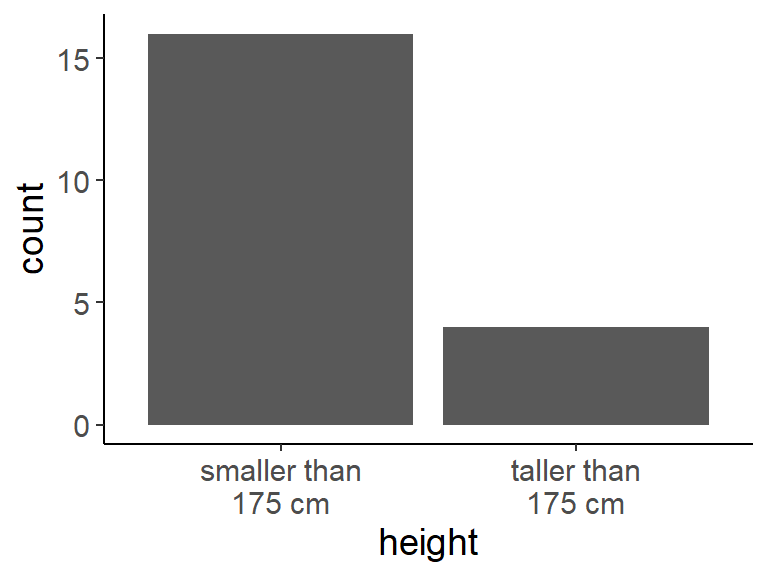
- How would you quantify the probability that someone in this room is taller than 175 cm if we pick someone randomly? Imagine 16 are smaller and 4 are taller than 175 cm.
- Solution: \(\frac{4}{16+4} = 0.2\)
4 Probability mass functions
- out of this example, we can constuct the probability mass function (pmf)
- the pmf is a function that gives the probability that a discrete random variable is exactly equal to some value
- the probabilties of all possible outcomes sum up to 1
5 Probability
- How would you quantify the probability that someone in this room is taller than 175 cm and smaller than 180 cm?
Code
heights <- c(162.5991, 169.7083, 154.8859, 176.9837, 152.9955,
166.7666, 170.8611, 156.8119, 152.9782, 181.7327,
166.3193, 162.3588, 163.0147, 175.8846, 164.3344,
171.851, 169.1128, 165.527, 179.5642, 157.6616)
ggplot() +
geom_histogram(aes(heights), breaks = seq(140, 195, 5)) +
annotate("rect", xmin = 175, xmax = 180, ymin = 0, ymax = 3,
fill = "blue", alpha = 0.7) +
scale_x_continuous(breaks = seq(140, 195, 5))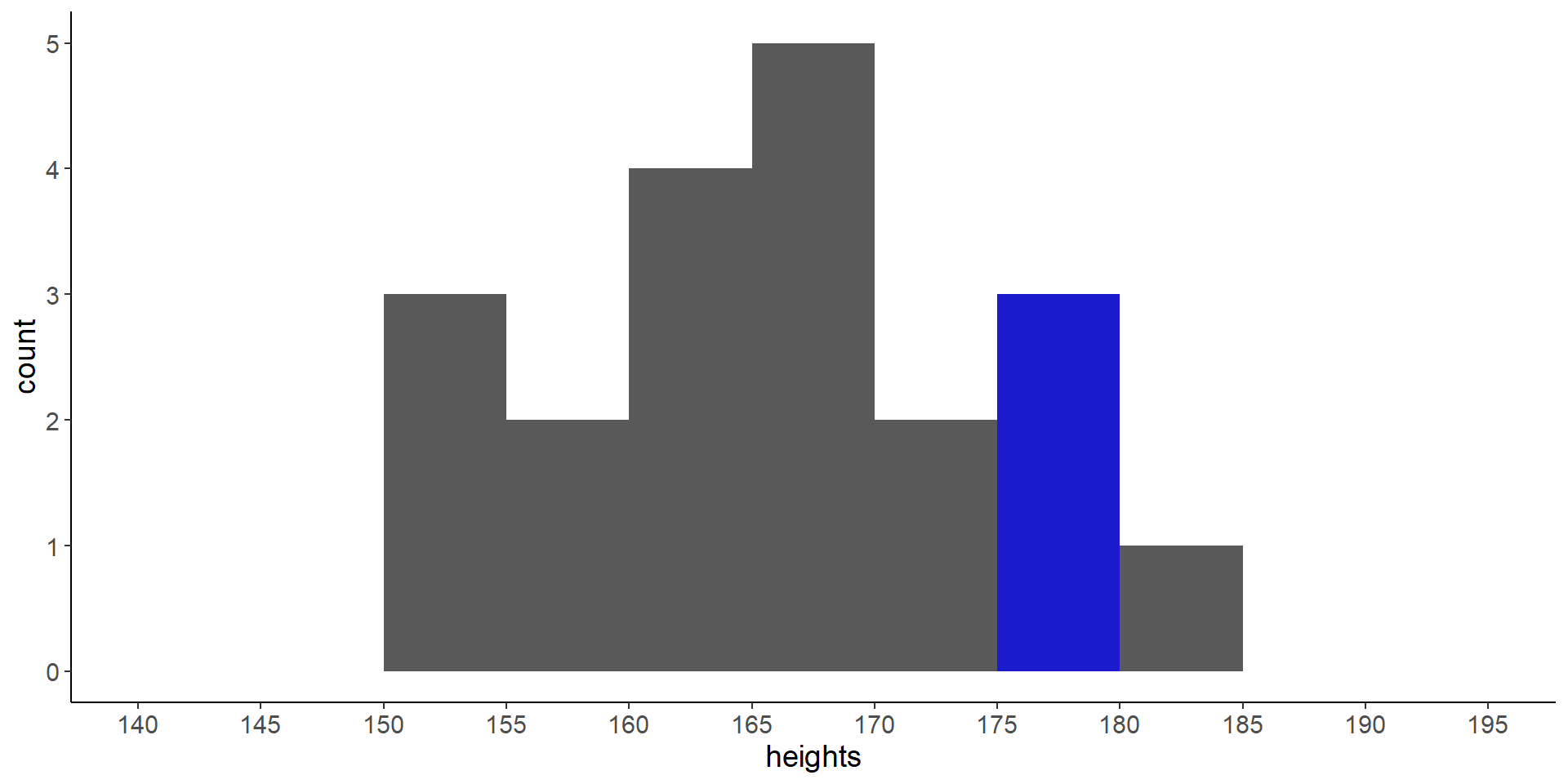
- the solution: \(\frac{3}{20} = 0.15\)
6 Probability mass function
- we can construct a probability mass function (pmf) and cumulative distribution function (cdf) for the discrete random variable
Code
df <- tibble(
height = seq(142.5, 192.5, 5.0),
count = as.numeric(
table(cut(heights, breaks = seq.int(from = 140, to = 195, by = 5)))),
pmf = count / sum(count),
cdf = cumsum(pmf)) %>%
select(-count) %>%
pivot_longer(c(pmf, cdf), names_to = "group", values_to = "y") %>%
mutate(y = y + 0.001,
group = factor(group, levels = c("pmf", "cdf")))
ggplot(aes(x = height, y = y), data = df) +
geom_col() +
scale_x_continuous(breaks = seq(140, 195, 5)) +
labs(y = "probability") +
facet_grid(group ~ .) +
theme_light() +
theme(text = element_text(size = 14))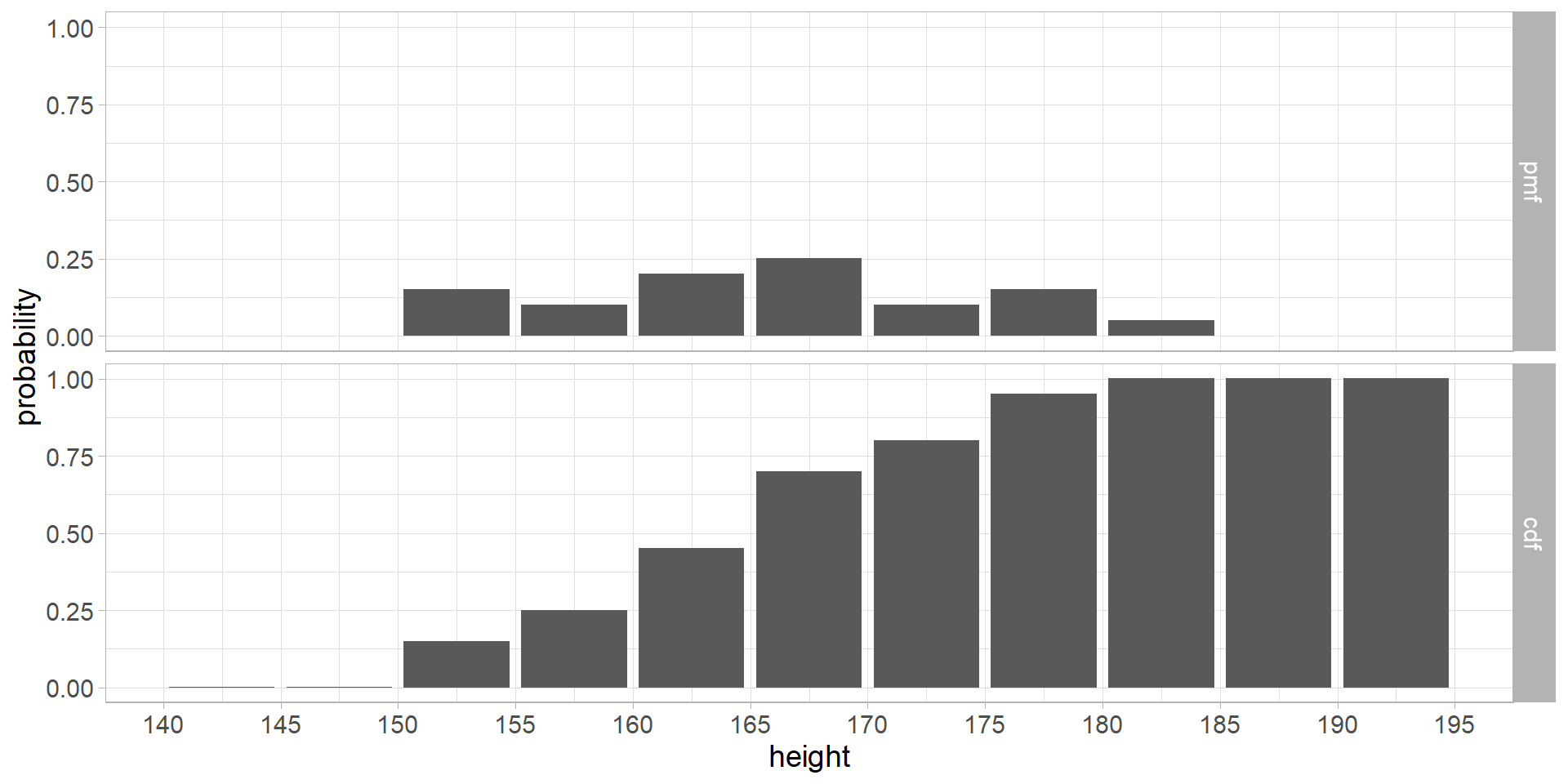
7 Problem with discrete random variables
- but what is the probability that a person is between 185 cm and 190 cm tall?
- the discrete distribution does not look generizable to the whole population
8 Let’s use a continous distribution
Code
lm1 <- lm(heights ~ 1)
sd1 <- sigma(lm1) # equivalent to sd(heights)
m1 <- coef(lm1) # equivalent to mean(heights)
df <- tibble(
height = seq(142.5, 192.5, 5.0),
count = as.numeric(
table(cut(heights, breaks = seq.int(from = 140, to = 195, by = 5)))),
density = count / sum(count))
df_norm <- tibble(
height = seq(140, 195, length.out = 200),
density = dnorm(height, mean = m1, sd = sd1))
ggplot() +
geom_col(aes(y = density, x = height), width = 4.8, data = df) +
geom_point(aes(x = height, y = 0.008), data = tibble(height = heights),
size = 4,
alpha = 0.6, color = "blue",
position = position_jitter(seed = 2, width = 0, height = 0.008)) +
geom_line(aes(x = height, y = density), data = df_norm, linewidth = 2, color = "red") +
scale_x_continuous(breaks = seq(140, 195, 5)) +
labs(y = "density / probability")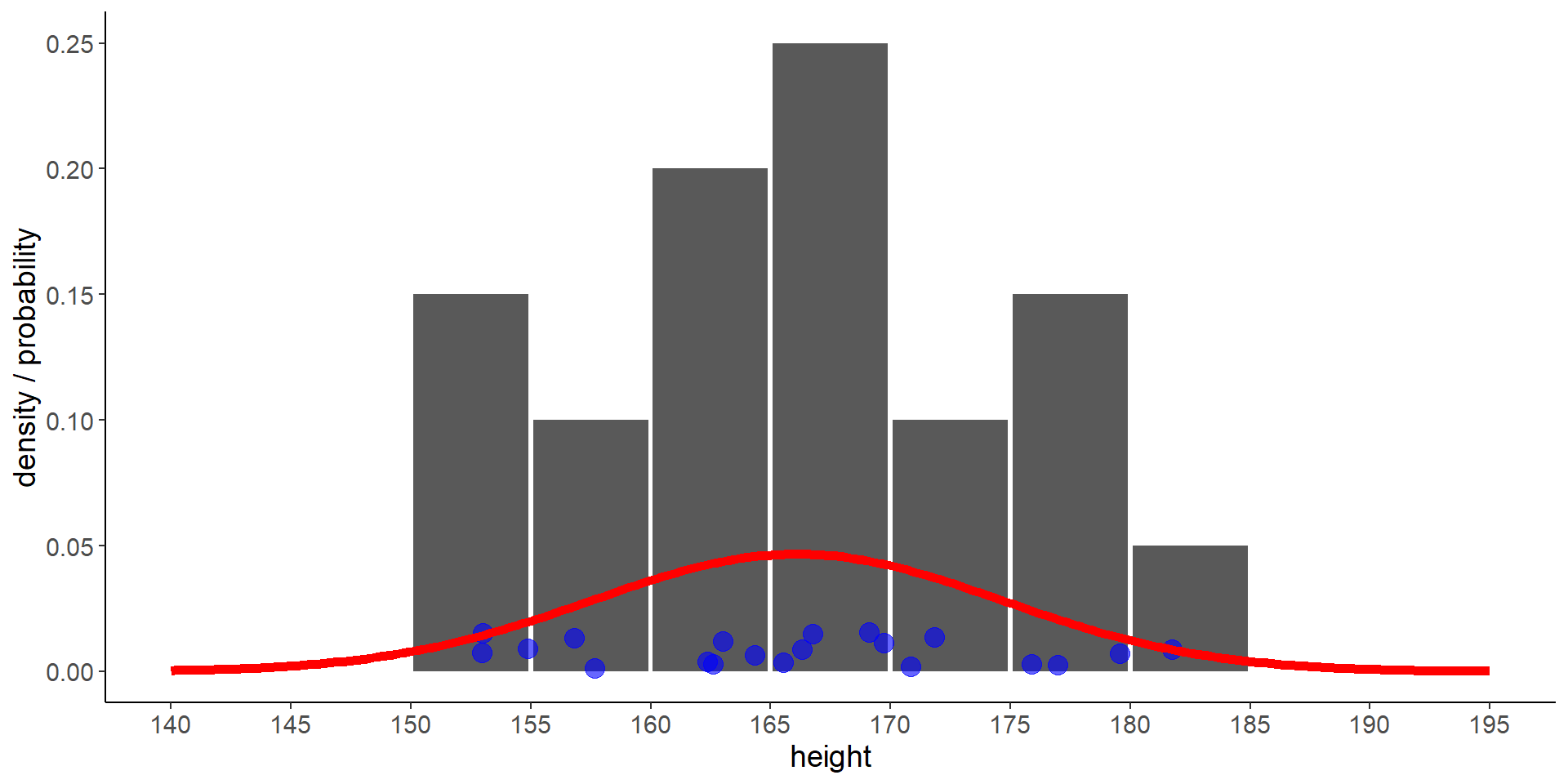
9 Probability for continous distributions
- what is the probability that a person is between 185 cm and 190 cm tall?
- in contrast to discrete distributions, we have to calculate the area under the curve of the probability density function (pdf) to get the probability
Code
ggplot() +
geom_ribbon(aes(x = height, ymin = 0, ymax = density),
data = filter(df_norm, height >= 185 & height <= 190),
fill = "purple", alpha = 0.5) +
geom_line(aes(x = height, y = density), data = df_norm,
color = "red", linewidth = 2) +
scale_x_continuous(breaks = seq(140, 195, 5))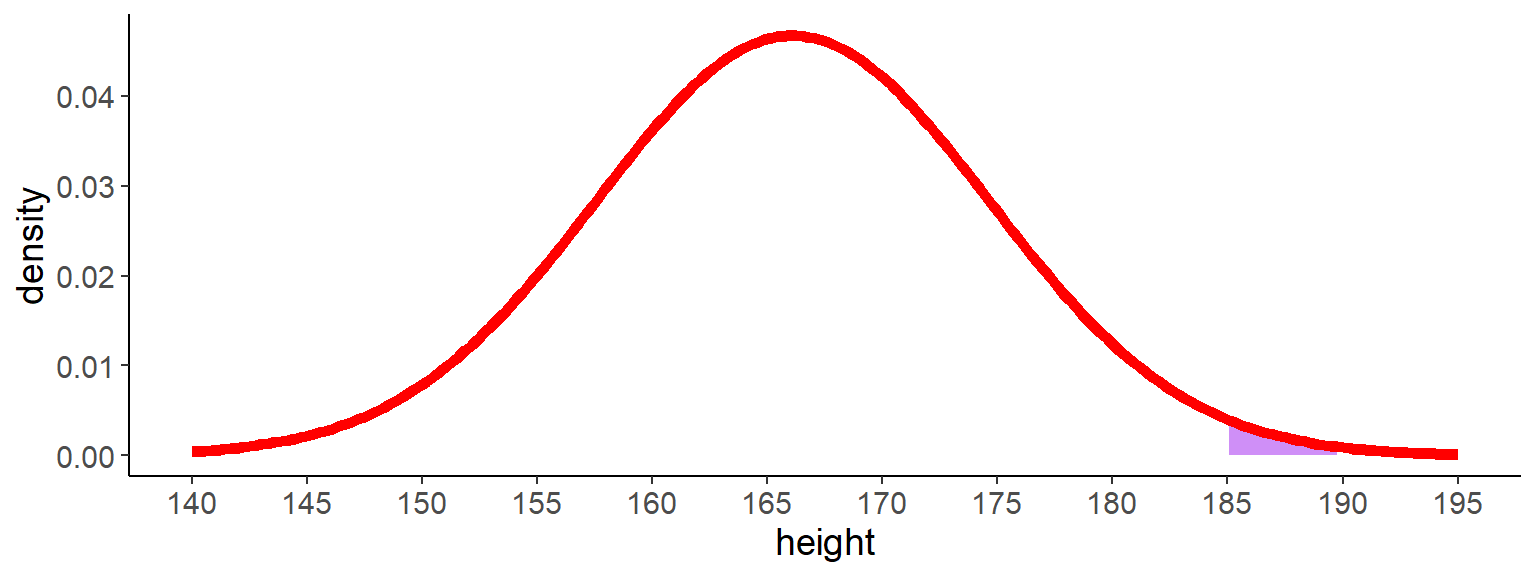
Note
Probability density functions are used for continous distributions, probability mass functions for discrete distributions.
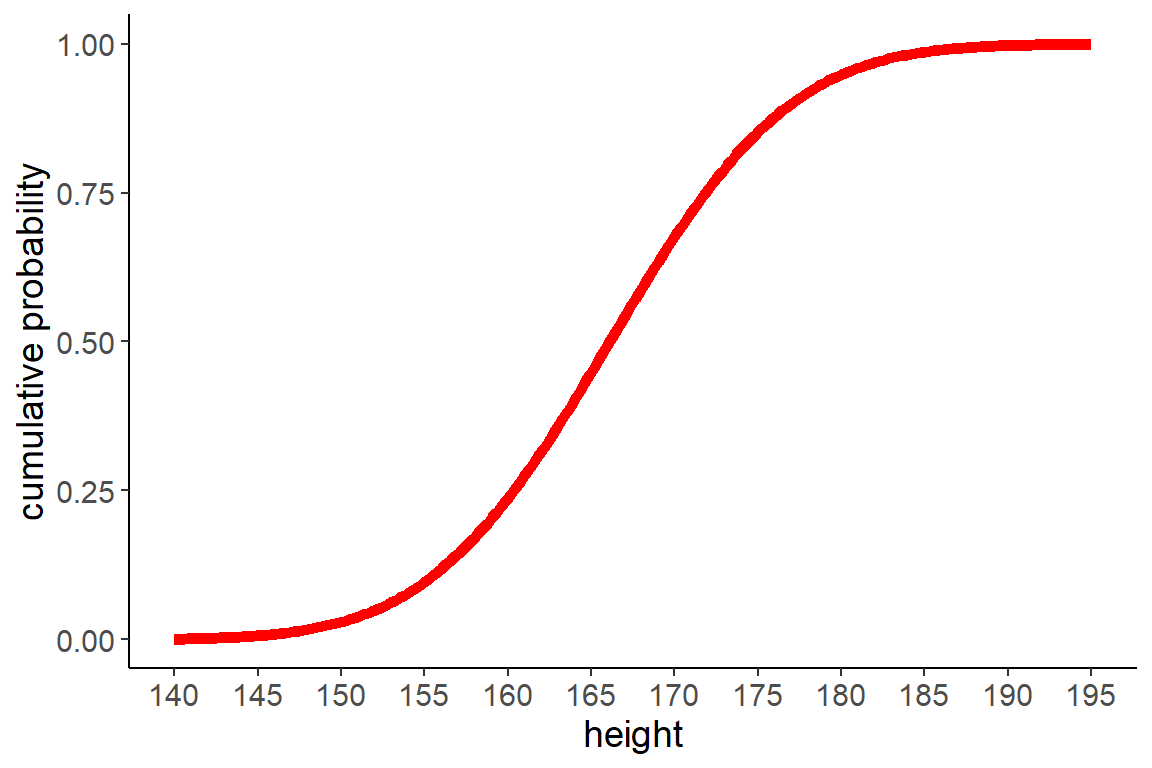
10 Cumulative distribution function
- the cumulative distribution function (cdf) for a continous distribution sums up the probability of all values smaller than a given value \(x\)
- the cdf is the integral (sums up the area under the curve) of the pdf
11 Finally, let’s calculate the probability
- we wanted to know the probability that a person is between 185 cm and 190 cm tall
- we can calculate this by subtracting the cdf at 185 cm from the cdf at 190 cm
- this is the same as calculating definite integrals, which you may have learnt at school
12 What did we do?
- we fitted the (continuous) normal distribution to the data
- we can calculate the probability that a person is between a and b cm tall
in math notation, height is normally distributed with mean \(\mu\) and standard deviation \(\sigma\):
\[ \text{height} \sim \mathcal{N}(\mu, \sigma) \]
13 What else can we do with a (Normal) distribution
Tip: Distribution zoo
the distribution zoo is a great tool to explore different distributions and what you can do with them
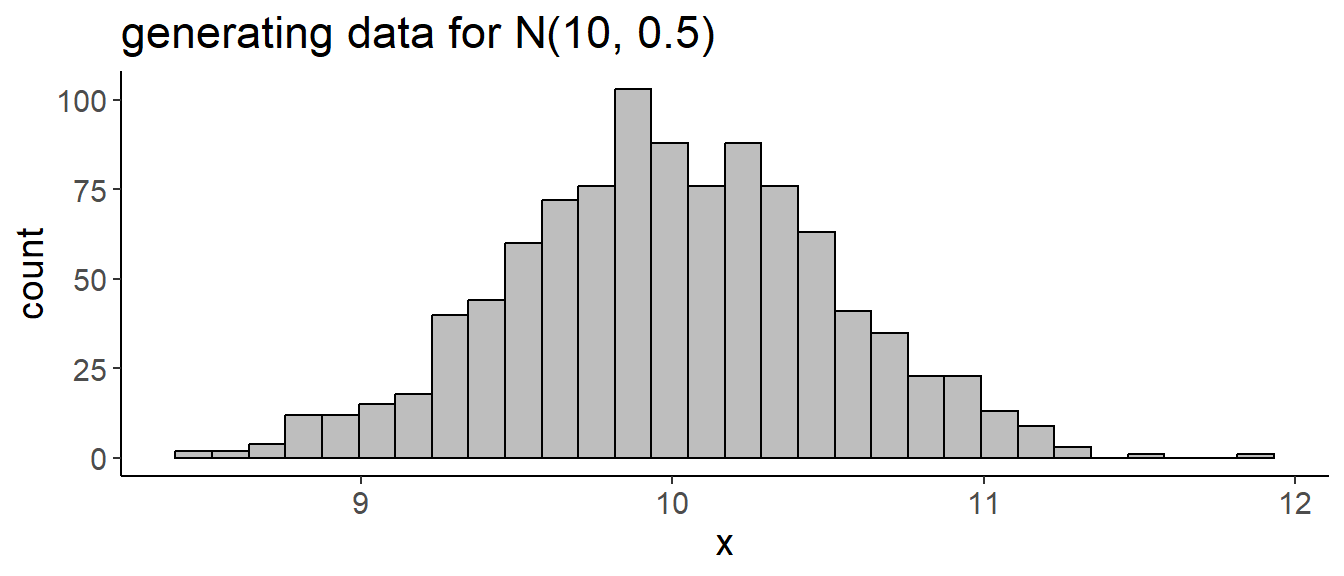
we can generate random numbers from a fitted distribution:
we can ask how tall a person is that is the 70 % percentile of the population:
- we use the inverse cumulative distribution function (quantile function) to calculate this:
qnorm(0.7, mean = 166, sd = 8)[1] 170.195214 But how do we fit a distribution to data?
let’s start with fitting the mean \(\mu\) to the data:
Code
df <- tibble(height = heights)
some_distributions <- tibble(
height = seq(140, 195, length.out = 200),
`150` = dnorm(height, mean = 150, sd = 10),
`166` = dnorm(height, mean = 166, sd = 10),
`180` = dnorm(height, mean = 180, sd = 10)) %>%
pivot_longer(-height, names_to = "name", values_to = "y")
ggplot() +
geom_point(aes(x = height, y = 0.001), data = df,
size = 4,
alpha = 0.6, color = "blue",
position = position_jitter(seed = 2, width = 0, height = 0.001)) +
geom_line(aes(x = height, y = y, color = name), data = some_distributions,
linewidth = 2) +
labs(y = "density",
title = "Which distribution fits the data best?",
color = "Mean")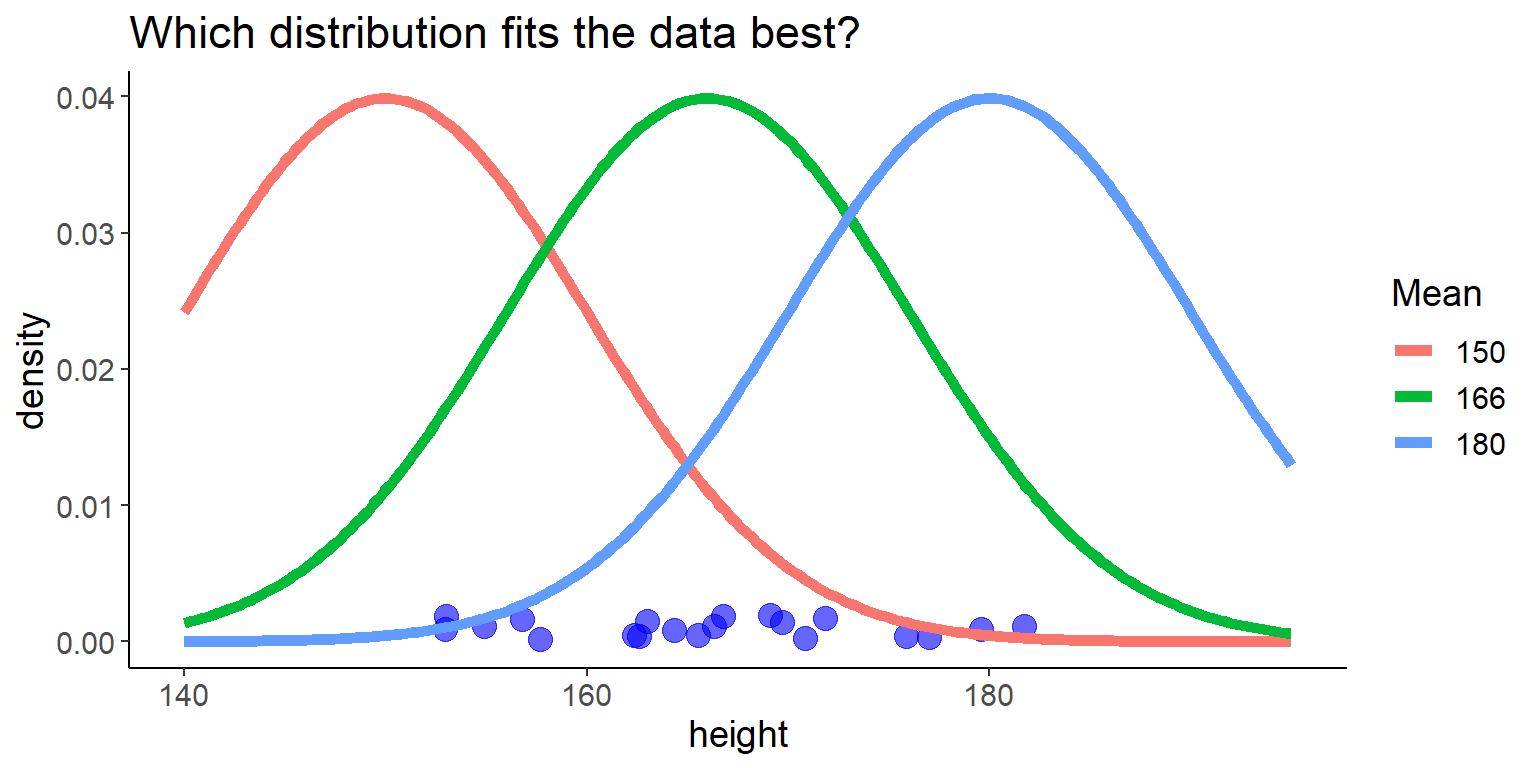
now, we fit the standard deviation \(\sigma\):
Code
some_distributions <- tibble(
height = seq(140, 195, length.out = 200),
`2` = dnorm(height, mean = 166, sd = 2),
`10` = dnorm(height, mean = 166, sd = 10),
`20` = dnorm(height, mean = 166, sd = 20)) %>%
pivot_longer(-height, names_to = "name", values_to = "y") %>%
mutate(name = fct_reorder(name, as.numeric(name)))
ggplot() +
geom_point(aes(x = height, y = 0.001), data = df,
size = 4,
alpha = 0.6, color = "blue",
position = position_jitter(seed = 2, width = 0, height = 0.001)) +
geom_line(aes(x = height, y = y, color = name), data = some_distributions,
linewidth = 2) +
labs(y = "density",
title = "Which distribution fits the data best?",
color = "Standard\n deviation")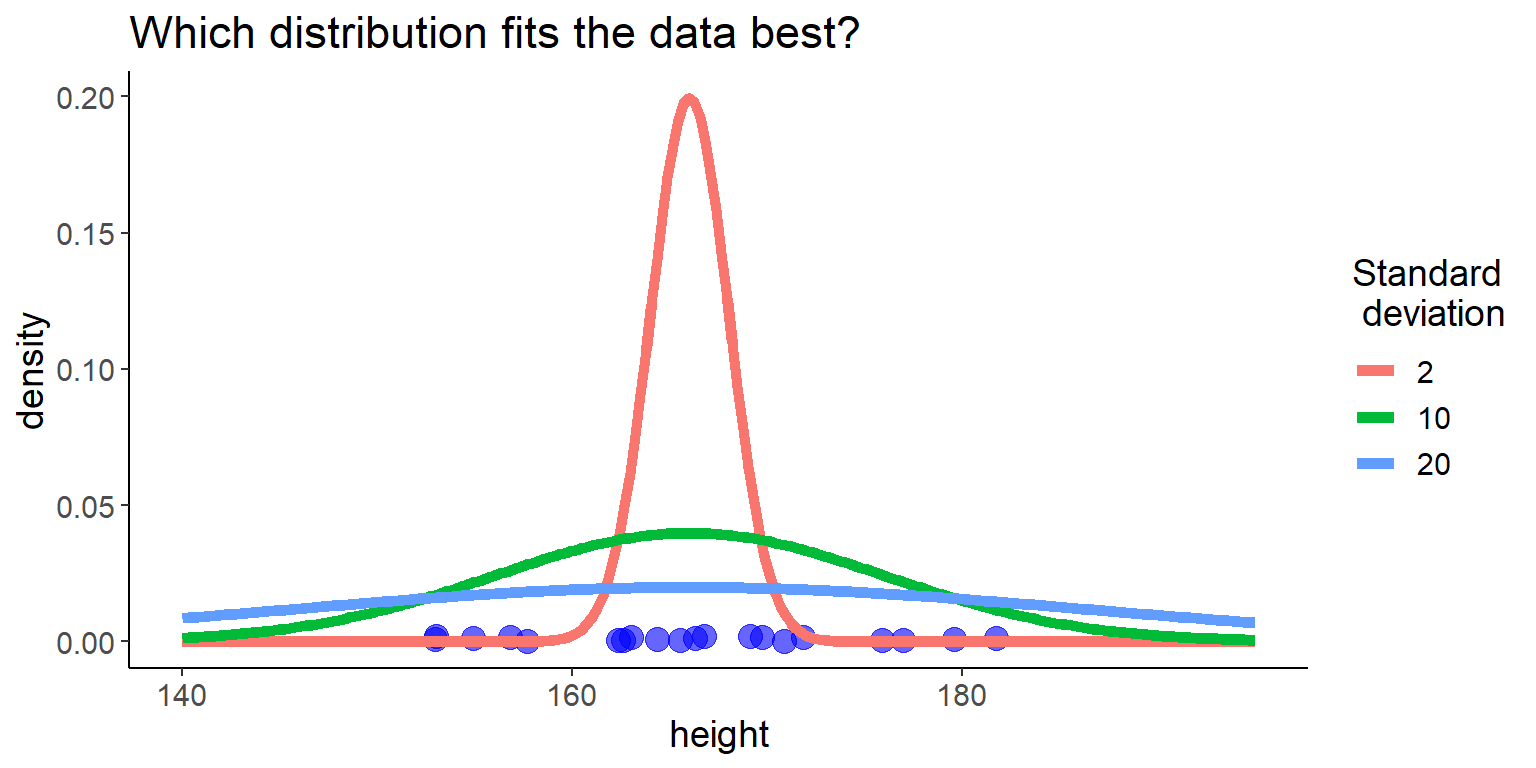
15 Likelihood
- more formally, we can use the likelihood to fit a distribution to data
- the likelihood is the product of the density (or probability) of each data point \(x_i\) given the parameters of the distribution
- in our case of the normal distribution, we can write the likelihood as:
\[ \mathcal{L}(\mu, \sigma) = \prod_{i=1}^n p(x_i| \mu, \sigma) \]
16 Likelihood visualization
- we calculate the likelihood given our data for \(\mathcal{N}(\mu = 170,\,\sigma = 10)\)
Code
df <- tibble(height = heights)
mu <- 170
sigma <- 10
likelihood_df <- tibble(
height = heights,
density = dnorm(height, mean = mu, sd = sigma))
dens_df <- tibble(
height = seq(140, 195, length.out = 200),
density = dnorm(height, mean = mu, sd = sigma))
ggplot(aes(x = height, y = 0), data = df) +
geom_line(aes(y = density), data = dens_df,
color = "red", linewidth = 2) +
geom_point(size = 3, color = "blue", alpha = 0.6) +
labs(y = "density")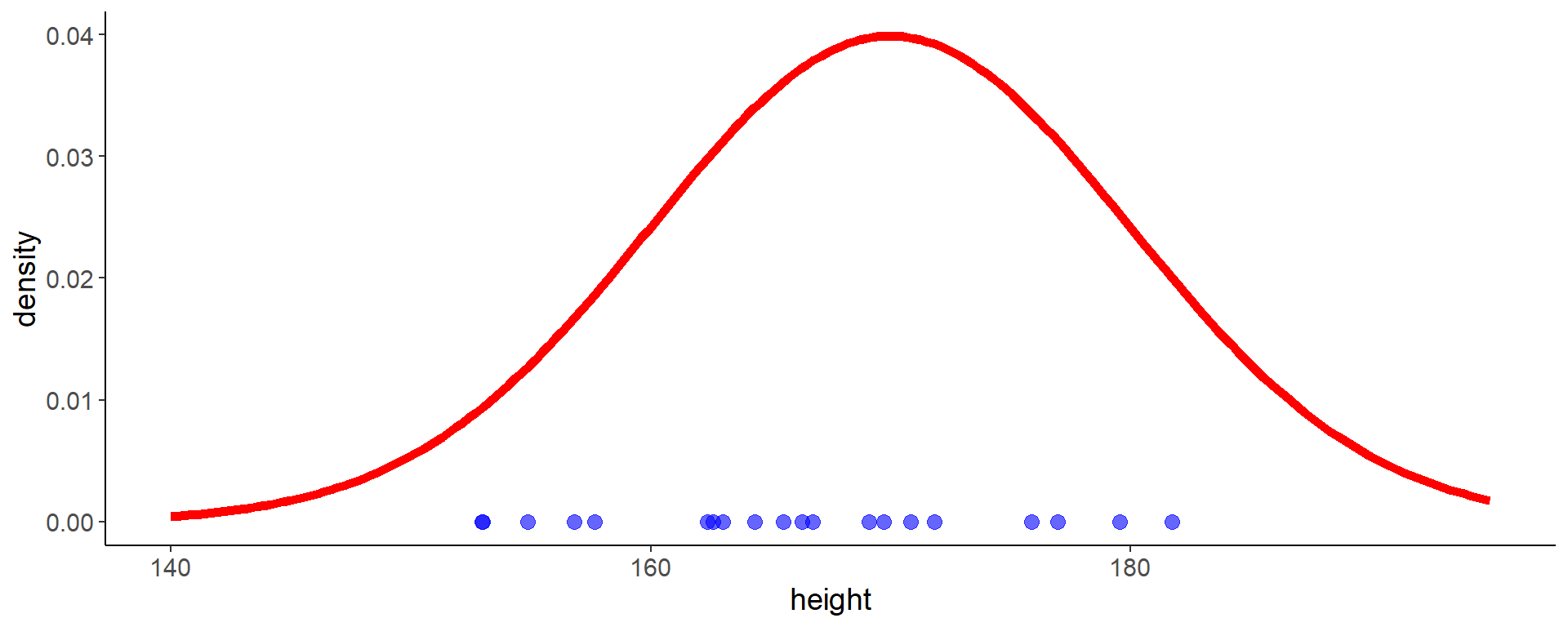
Code
ggplot(aes(x = height, y = 0), data = df) +
geom_line(aes(y = density), data = dens_df,
color = "red", linewidth = 2) +
geom_segment(aes(x = height, xend = height, y = 0, yend = density),
data = filter(likelihood_df, height == min(height)),
color = "grey") +
geom_segment(aes(x = height, xend = 140, y = density, yend = density),
data = filter(likelihood_df, height == min(height)),
color = "grey") +
geom_point(size = 3, color = "blue", alpha = 0.6) +
labs(y = "density")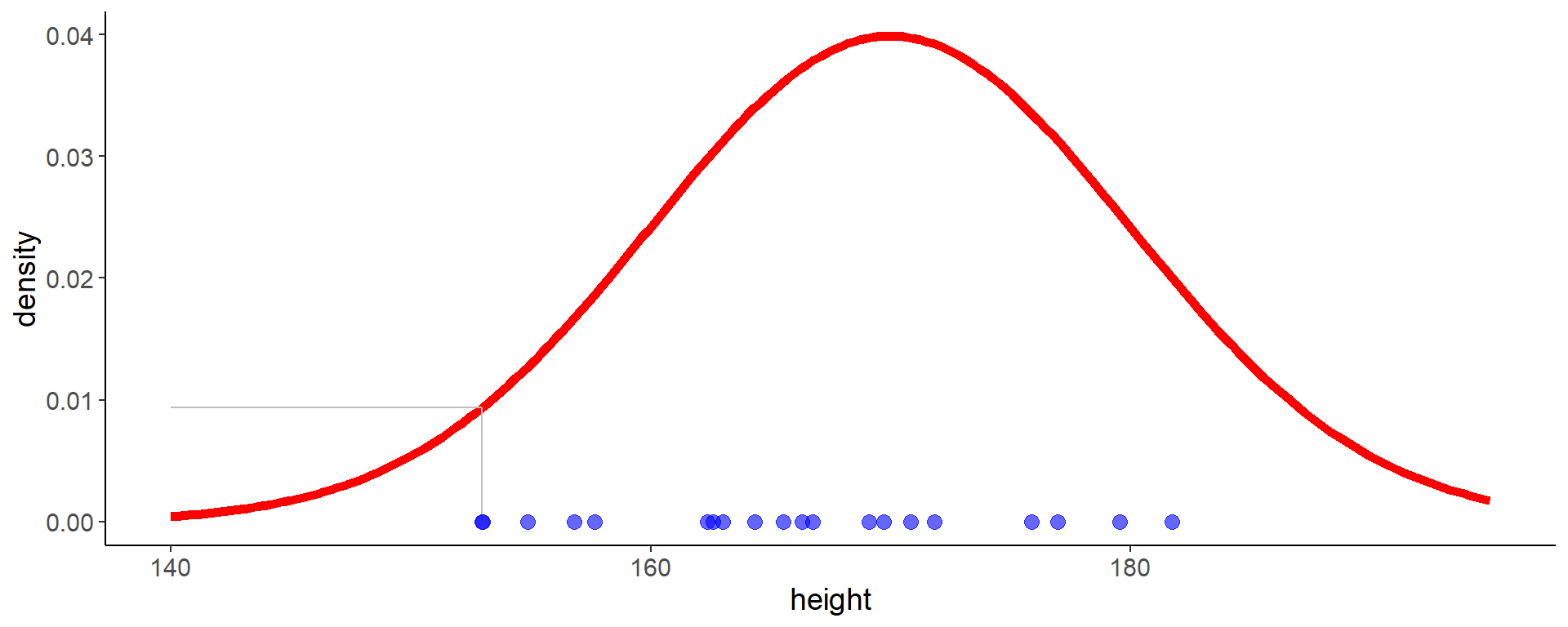
Code
ggplot(aes(x = height, y = 0), data = df) +
geom_line(aes(y = density), data = dens_df,
color = "red", linewidth = 2) +
geom_segment(aes(x = height, xend = height, y = 0, yend = density),
data = likelihood_df,
color = "grey") +
geom_segment(aes(x = height, xend = 140, y = density, yend = density),
data = likelihood_df,
color = "grey") +
geom_point(size = 3, color = "blue", alpha = 0.6) +
labs(y = "density")
17 How to interpret the likelihood?
- the value of the likelihood cannot be interpreted directly it is only useful for comparing different models
- because the likelihood is a product of densities (or probabilities), it can become very small, which is numerically difficult to handle
- therefore, we often use the log-likelihood, which is the sum of the log densities (probabilities) of the observations
18 Maximum likelihood estimation
- the goal is to find the parameters that maximize the likelihood
- the parameters are then called maximum likelihood estimates (MLEs)
- for some distributions, we can calculate the MLEs analytically, for others we have to use numerical optimization
19 Likelihood for different \(\mu\) and \(\sigma\)
Code
likelihoods_df <-
expand_grid(
mu = seq(130, 200, length = 400),
sigma = seq(0.1, 50, length = 400)) %>%
mutate(log_likelihood = map2_dbl(
mu, sigma,
~ sum(dnorm(heights, mean = .x, sd = .y, log = T)))) %>%
filter(log_likelihood >= quantile(log_likelihood, 0.5))
ggplot(likelihoods_df) +
geom_contour_filled(aes(mu, sigma, z = log_likelihood)) +
labs(x = "mean μ", y = "standard deviation σ", fill = "log-likelihood") +
annotate("point", x = mean(heights), y = sd(heights),
color = "red", size = 4) +
guides(fill = guide_legend(reverse = TRUE))
Note
The maximum likelihood estimate for a Normal distribution is the sample mean and sample standard deviation.
20 Which R functions can you use?
mu <- 2
sigma <- 3
# probability density function (pdf)
dnorm(x = 1, mean = mu, sd = sigma)[1] 0.1257944# cumulative distribution function (cdf)
pnorm(q = 2, mean = mu, sd = sigma)[1] 0.5# quantile function (inverse cdf)
qnorm(p = 0.5, mean = mu, sd = sigma)[1] 2# random number generator
rnorm(n = 5, mean = mu, sd = sigma)[1] 5.4048953 5.3357955 -0.6123329 2.6321948 2.2081869# maximum likelihood estimation
lm1 <- lm(height ~ 1, data = tibble(height = heights))
mle <- c(as.numeric(coef(lm1)), sigma(lm1)); names(mle) <- c("mu", "sigma")
mle mu sigma
166.097570 8.536452 21 Copy-paste the code
## load packages
library(dplyr)
library(tidyr)
library(stringr)
library(forcats)
library(purrr)
library(ggplot2)
## theme for ggplot
theme_set(theme_classic())
theme_update(text = element_text(size = 14))
## set seed for reproducibility (random numbers generation)
set.seed(1)
## bar plot with the number of people smaller and taller than 175 cm
taller_df <- tibble(
height = c(rep("smaller than\n175 cm", 16),
rep("taller than\n175 cm", 4)))
ggplot(taller_df, aes(height)) +
geom_bar()
## probability mass function out of the first plot
pmf_df <- tibble(
height = c("smaller than\n175.5 cm", "taller than\n175.5 cm"),
probability = c(16/(16+4), 4/(16+4)))
ggplot(pmf_df, aes(height, probability)) +
geom_col()
## histogram of the data
heights <- c(162.5991, 169.7083, 154.8859, 176.9837, 152.9955,
166.7666, 170.8611, 156.8119, 152.9782, 181.7327,
166.3193, 162.3588, 163.0147, 175.8846, 164.3344,
171.851, 169.1128, 165.527, 179.5642, 157.6616)
ggplot() +
geom_histogram(aes(heights), breaks = seq(140, 195, 5)) +
annotate("rect", xmin = 175, xmax = 180, ymin = 0, ymax = 3,
fill = "blue", alpha = 0.7) +
scale_x_continuous(breaks = seq(140, 195, 5))
## probability mass function and probability density function in one plot
df <- tibble(
height = seq(142.5, 192.5, 5.0),
count = as.numeric(
table(cut(heights, breaks = seq.int(from = 140, to = 195, by = 5)))),
pmf = count / sum(count),
cdf = cumsum(pmf)) %>%
select(-count) %>%
pivot_longer(c(pmf, cdf), names_to = "group", values_to = "y") %>%
mutate(y = y + 0.001,
group = factor(group, levels = c("pmf", "cdf")))
ggplot(aes(x = height, y = y), data = df) +
geom_col() +
scale_x_continuous(breaks = seq(140, 195, 5)) +
labs(y = "probability") +
facet_grid(group ~ .) +
theme_light() +
theme(text = element_text(size = 14))
## probability density function with probabilities of the intervals
lm1 <- lm(heights ~ 1)
sd1 <- sigma(lm1) # equivalent to sd(heights)
m1 <- coef(lm1) # equivalent to mean(heights)
df <- tibble(
height = seq(142.5, 192.5, 5.0),
count = as.numeric(
table(cut(heights, breaks = seq.int(from = 140, to = 195, by = 5)))),
density = count / sum(count))
df_norm <- tibble(
height = seq(140, 195, length.out = 200),
density = dnorm(height, mean = m1, sd = sd1))
ggplot() +
geom_col(aes(y = density, x = height), width = 4.8, data = df) +
geom_point(aes(x = height, y = 0.008), data = tibble(height = heights),
size = 4,
alpha = 0.6, color = "blue",
position = position_jitter(seed = 2, width = 0, height = 0.008)) +
geom_line(aes(x = height, y = density), data = df_norm, linewidth = 2, color = "red") +
scale_x_continuous(breaks = seq(140, 195, 5)) +
labs(y = "density / probability")
## Area under curve for continous distribution = probabilities
ggplot() +
geom_ribbon(aes(x = height, ymin = 0, ymax = density),
data = filter(df_norm, height >= 185 & height <= 190),
fill = "purple", alpha = 0.5) +
geom_line(aes(x = height, y = density), data = df_norm,
color = "red", linewidth = 2) +
scale_x_continuous(breaks = seq(140, 195, 5))
## cumulative distribution function
df <- tibble(
height = seq(140, 195, length.out = 200),
cdf = pnorm(height, mean = m1, sd = sd1))
ggplot(df, aes(height, cdf)) +
geom_line(color = "red", linewidth = 2) +
scale_x_continuous(breaks = seq(140, 195, 5)) +
labs(y = "cumulative probability")
## calculate probability
pnorm(190, mean = m1, sd = sd1) - pnorm(185, mean = m1, sd = sd1)
## generate random numbers
df <- tibble(x = rnorm(1000, mean = 10, sd = 0.5))
ggplot(df, aes(x)) +
geom_histogram(bins = 30, fill = "grey", color = "black") +
labs(title = "generating data for N(10, 0.5)")
## fit mean of distribution to data
df <- tibble(height = heights)
some_distributions <- tibble(
height = seq(140, 195, length.out = 200),
`150` = dnorm(height, mean = 150, sd = 10),
`166` = dnorm(height, mean = 166, sd = 10),
`180` = dnorm(height, mean = 180, sd = 10)) %>%
pivot_longer(-height, names_to = "name", values_to = "y")
ggplot() +
geom_point(aes(x = height, y = 0.001), data = df,
size = 4,
alpha = 0.6, color = "blue",
position = position_jitter(seed = 2, width = 0, height = 0.001)) +
geom_line(aes(x = height, y = y, color = name), data = some_distributions,
linewidth = 2) +
labs(y = "density",
title = "Which distribution fits the data best?",
color = "Mean")
## fit standard deviation of distribution to data
some_distributions <- tibble(
height = seq(140, 195, length.out = 200),
`2` = dnorm(height, mean = 166, sd = 2),
`10` = dnorm(height, mean = 166, sd = 10),
`20` = dnorm(height, mean = 166, sd = 20)) %>%
pivot_longer(-height, names_to = "name", values_to = "y") %>%
mutate(name = fct_reorder(name, as.numeric(name)))
ggplot() +
geom_point(aes(x = height, y = 0.001), data = df,
size = 4,
alpha = 0.6, color = "blue",
position = position_jitter(seed = 2, width = 0, height = 0.001)) +
geom_line(aes(x = height, y = y, color = name), data = some_distributions,
linewidth = 2) +
labs(y = "density",
title = "Which distribution fits the data best?",
color = "Standard\n deviation")
## visualize likelihood
df <- tibble(height = heights)
mu <- 170
sigma <- 10
likelihood_df <- tibble(
height = heights,
density = dnorm(height, mean = mu, sd = sigma))
dens_df <- tibble(
height = seq(140, 195, length.out = 200),
density = dnorm(height, mean = mu, sd = sigma))
ggplot(aes(x = height, y = 0), data = df) +
geom_line(aes(y = density), data = dens_df,
color = "red", linewidth = 2) +
geom_segment(aes(x = height, xend = height, y = 0, yend = density),
data = likelihood_df,
color = "grey") +
geom_segment(aes(x = height, xend = 140, y = density, yend = density),
data = likelihood_df,
color = "grey") +
geom_point(size = 3, color = "blue", alpha = 0.6) +
labs(y = "density")
## likelihood for different mu and sigma
likelihoods_df <-
expand_grid(
mu = seq(130, 200, length = 400),
sigma = seq(0.1, 50, length = 400)) %>%
mutate(log_likelihood = map2_dbl(
mu, sigma,
~ sum(dnorm(heights, mean = .x, sd = .y, log = T)))) %>%
filter(log_likelihood >= quantile(log_likelihood, 0.5))
ggplot(likelihoods_df) +
geom_contour_filled(aes(mu, sigma, z = log_likelihood)) +
labs(x = "mean μ", y = "standard deviation σ", fill = "log-likelihood") +
annotate("point", x = mean(heights), y = sd(heights),
color = "red", size = 4) +
guides(fill = guide_legend(reverse = TRUE))
## which R can you use?
mu <- 2
sigma <- 3
# probability density function (pdf)
dnorm(x = 1, mean = mu, sd = sigma)
# cumulative distribution function (cdf)
pnorm(q = 2, mean = mu, sd = sigma)
# quantile function (inverse cdf)
qnorm(p = 0.5, mean = mu, sd = sigma)
# random number generator
rnorm(n = 5, mean = mu, sd = sigma)
# maximum likelihood estimation
lm1 <- lm(height ~ 1, data = tibble(height = heights))
mle <- c(as.numeric(coef(lm1)), sigma(lm1)); names(mle) <- c("mu", "sigma")
mleProbability and likelihood