library(tidyr)
library(dplyr)
library(ggplot2)
library(readr)
library(forcats)
library(ggfortify)
library(MASS)
## theme for ggplot
theme_set(theme_classic())
theme_update(text = element_text(size = 14))GLMs for count and proportion data
Day 8
Freie Universität Berlin @ Theoretical Ecology
Reproduce slides
Common data types in biology
Count data
- No. of discrete objects/events counted in a given constant time, area, volume, distance, sampling effort …
- Example: No. of individuals or no. of species in sample squares
Proportion / binary data
- Events/variables with only two potential values, e.g.:
- Dead / alive
- Present / absent
- Male / female
- Proportion of events with each of the two potential outcomes
Food for thought
Think about examples for count, proportion, and binary data in your favourite sub-field of Biology!
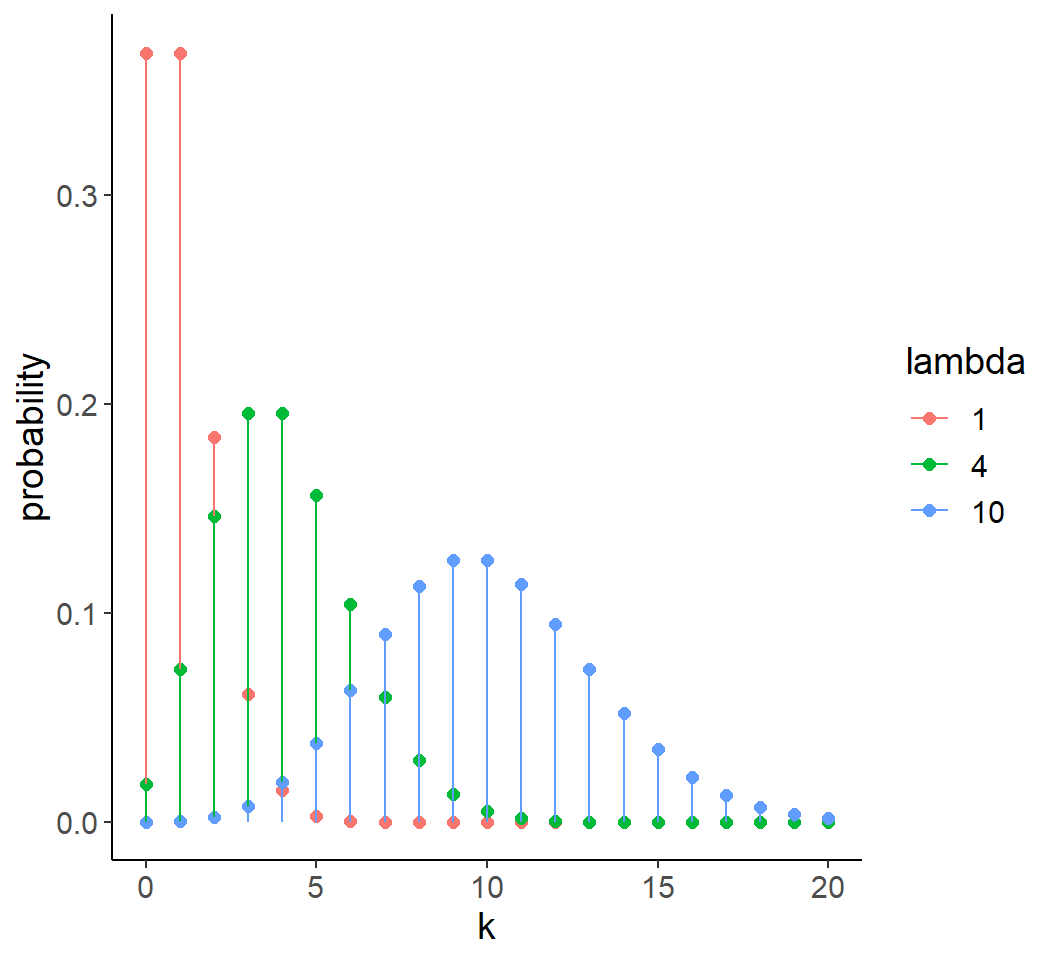
Count data
- Often described by Poisson distribution
- Discrete values and bounded:
- Y > 0
- \(\text{mean}(Y) = \text{var}(Y) = \lambda\)
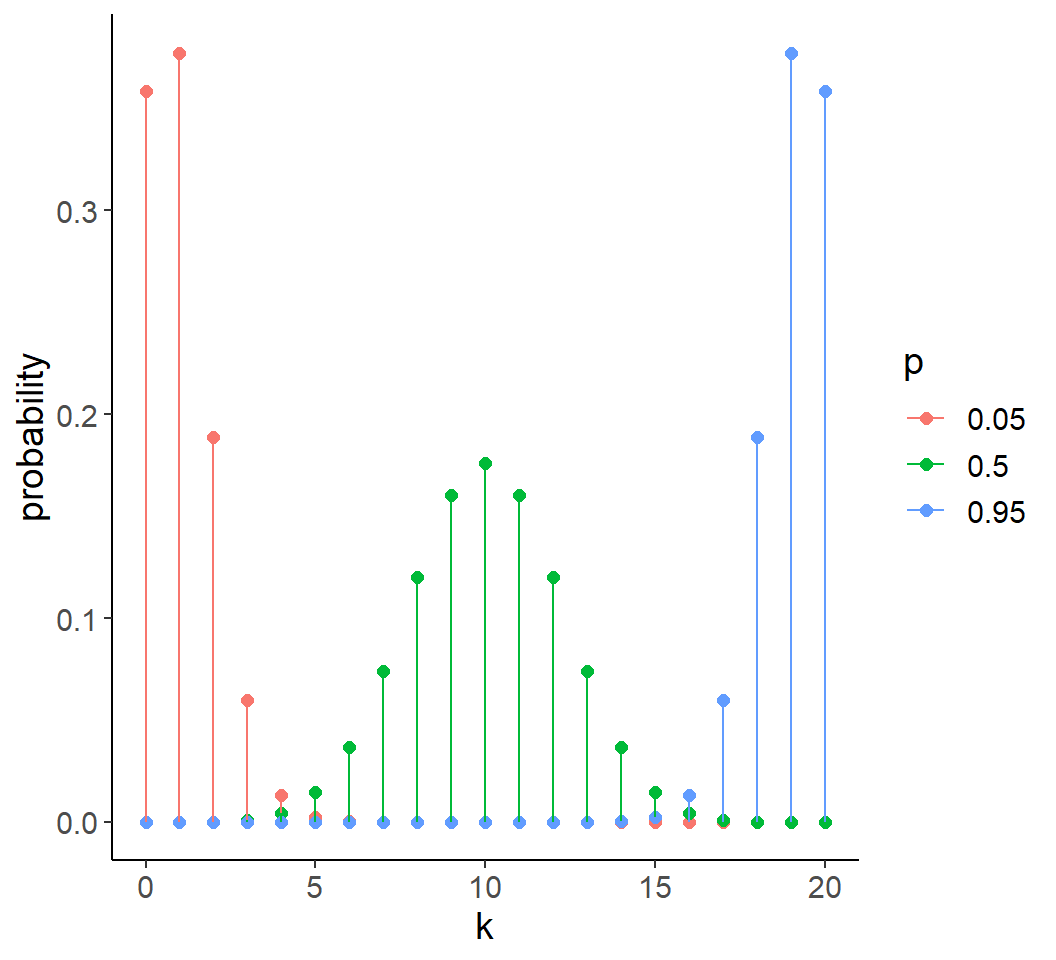
Proportion and binary data
- Often described by Binomial distribution
- Discrete values and bounded in interval [0, 1]
- \(\text{mean}(Y) = Np\)
- \(\text{var}(Y) = Np(1-p) = Np - Np^2\)
Assumptions of Linear Models
- Linear relationship between X and Y
- Normally distributed errors (residuals)
- Errors & response are not bounded \([-\infty, \infty]\)
- Constant variance of the residuals
- No relationship between mean(Y) and var(Y)
Linear models not appropriate for count, proportion and binary data!
The idea of GLMs
- Move from distributions to models
- The mean of the response \(y_i\) for data point \(i\) varies as (non-linear) function of the explanatory variables \(X_j\)
- Count data
- \(\lambda_i = f(X_j)\)
Code
soil_moisture <- runif(n = 50, min = 10, max = 50)
a <- -2
b <- 0.1
lin_pred <- a + soil_moisture*b
lambda <- exp(lin_pred)
y <- rpois(length(lambda), lambda = lambda)
dat1 <- tibble(soil_moisture,
no_of_seedlings = y)
ggplot(dat1, aes(soil_moisture, no_of_seedlings)) +
geom_point(size = 3, col = "seagreen") +
xlab("Soil moisture") +
ylab("No. of seedlings") +
geom_smooth(method = "glm", method.args = list(family = "poisson"),
color = "red")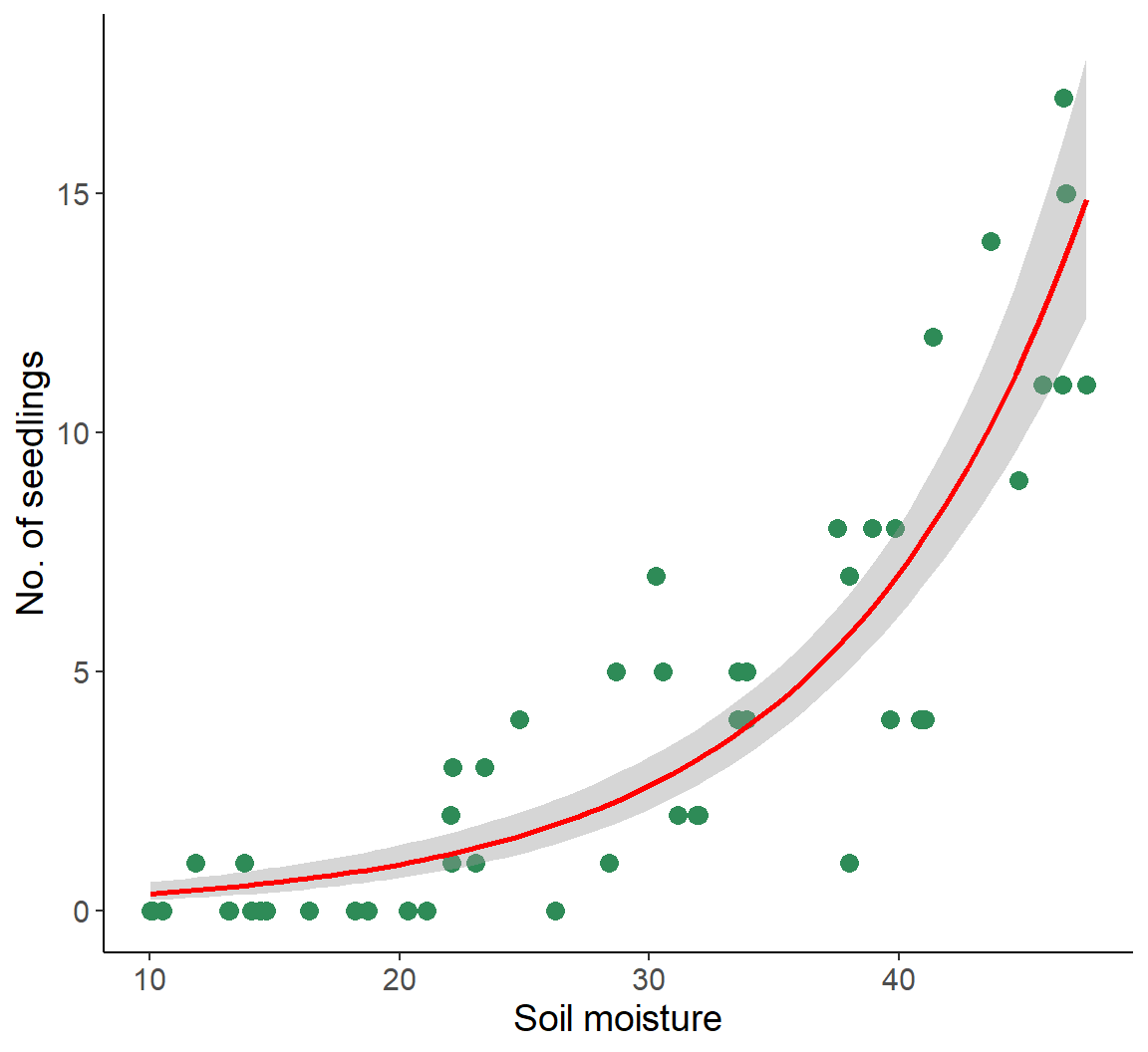
The idea of GLMs
- Proportion data
- \(p_i = f(X_j)\)
- \(N\) is defined by the data (see examples)
Code
no_of_seeds <- rep(seq(10, 100, by = 10), each = 6)
a <- 7
b <- -0.12
lin_pred <- a + no_of_seeds*b
pi <- exp(lin_pred)/(1 + exp(lin_pred))
y <- rbinom(length(pi), size = no_of_seeds, prob = pi)
dat1 <- tibble(no_of_seeds,
no_of_seedlings = y) %>%
mutate(prop_germinated = no_of_seedlings / no_of_seeds)
ggplot(dat1, aes(no_of_seeds, prop_germinated)) +
geom_point(size = 3, col = "skyblue3") +
xlab("No. of seeds") +
ylab("Proportion of germinated seeds") +
ggtitle("Density dependent germination rate") +
geom_smooth(method = "glm", method.args = list(family = "binomial"),
color = "red")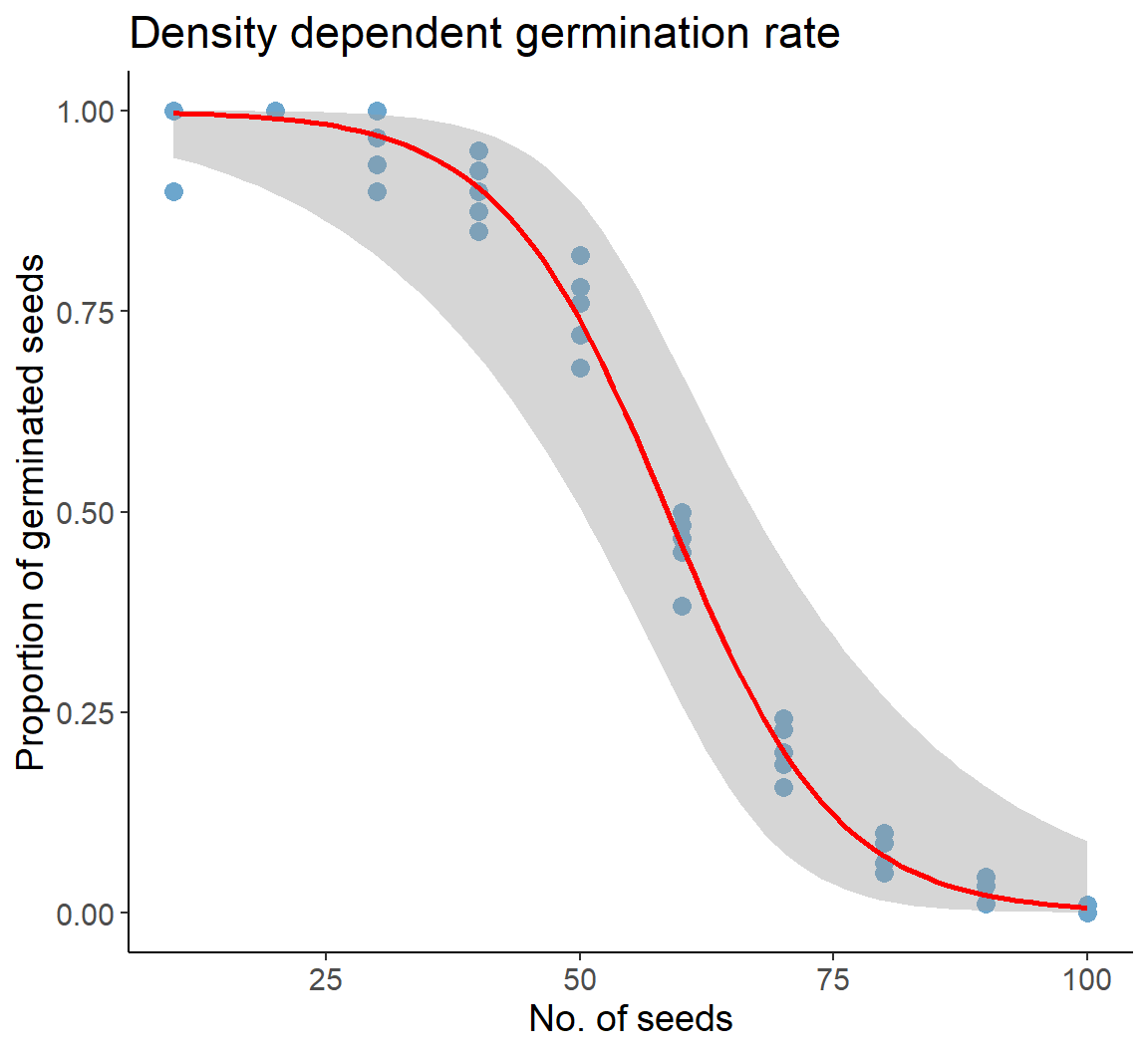
Generalized Linear Models – GLMs
Starting point: Linear models
\[y_i \sim \mathcal{N}(\mu_i, \sigma^2)\]
\[\mu_i = \alpha + \sum \beta_j x_{i,j}\]
GLM: 3 components
- Non-normal distribution error distribution
- Poisson distribution: \(y_i \sim \mathcal{P}(\lambda_i)\)
- Binomial distribution: \(y_i \sim \mathcal{B}(p_i, N_i)\)
Like in LM: Linear combination of the effects of the predictors \(X_j\)
\[\eta_i = \alpha + \sum{\beta_j x_{i,j}}\]
Links the mean response \((\mu_i)\) to the linear predictor \((\eta_i)\): \(g(\mu_i) = \eta_i\)
Inverse link function converts linear predictor to response: \(\mu_i = g^-1(\eta_i)\)
Count data: log-link function
Code
dat <- tibble(x = seq(0,10, by = 0.01),
y = log(x))
ggplot(dat, aes(x,y)) +
geom_line() +
ggtitle("η = log(𝛌)") +
theme(plot.title = element_text(hjust = 0.5)) +
geom_hline(yintercept = 0, linetype = 2) +
geom_vline(xintercept = 0, linetype = 2) +
xlab("𝛌 - mean response") +
ylab("η - linear predictor")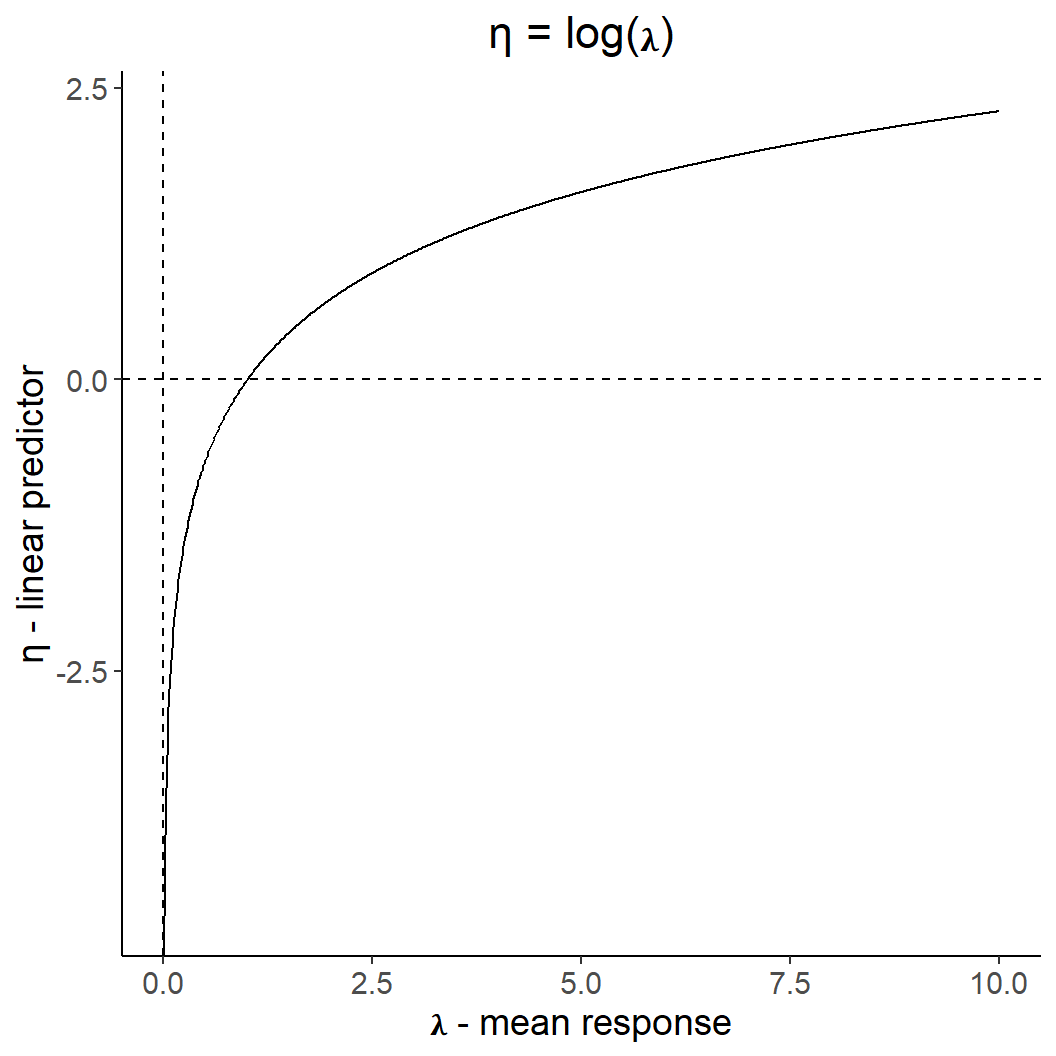
Code
dat <- tibble(x = seq(-2,4, by = 0.01),
y = exp(x))
ggplot(dat, aes(x,y)) +
geom_line() +
ggtitle("𝛌 = exp(η)") +
theme(plot.title = element_text(hjust = 0.5)) +
geom_hline(yintercept = 0, linetype = 2) +
geom_vline(xintercept = 0, linetype = 2) +
xlab("η - linear predictor" ) +
ylab("𝛌 - mean response")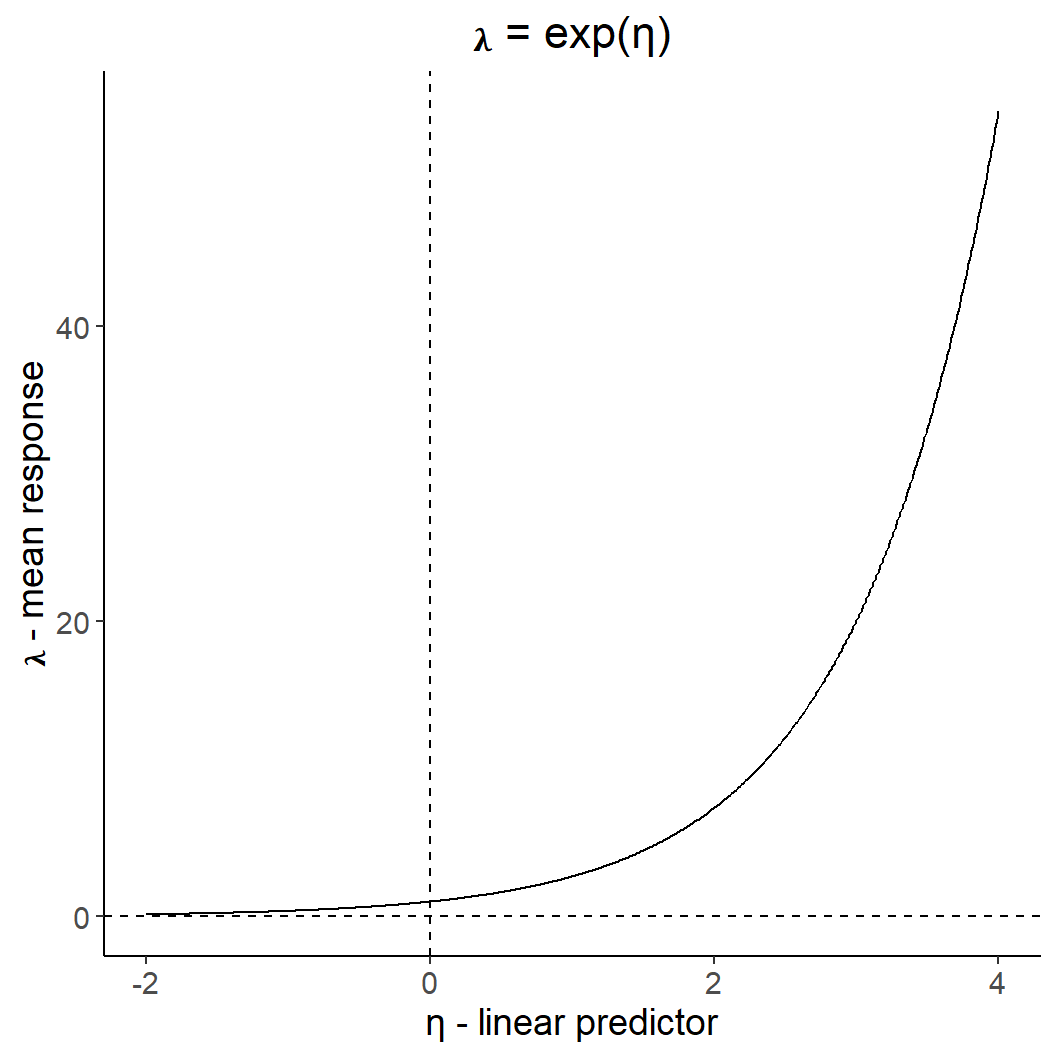
Proportion/ binary data: logit-link
Code
dat <- tibble(p = seq(0,1, by = 0.001),
y = log(p / (1 - p)))
ggplot(dat, aes(p,y)) +
geom_line() +
ggtitle("η = logit(p) = log(p / (1 - p))") +
theme(plot.title = element_text(hjust = 0.5)) +
geom_hline(yintercept = 0, linetype = 2) +
geom_vline(xintercept = 0, linetype = 2) +
xlab("p - mean response") +
ylab("η - linear predictor")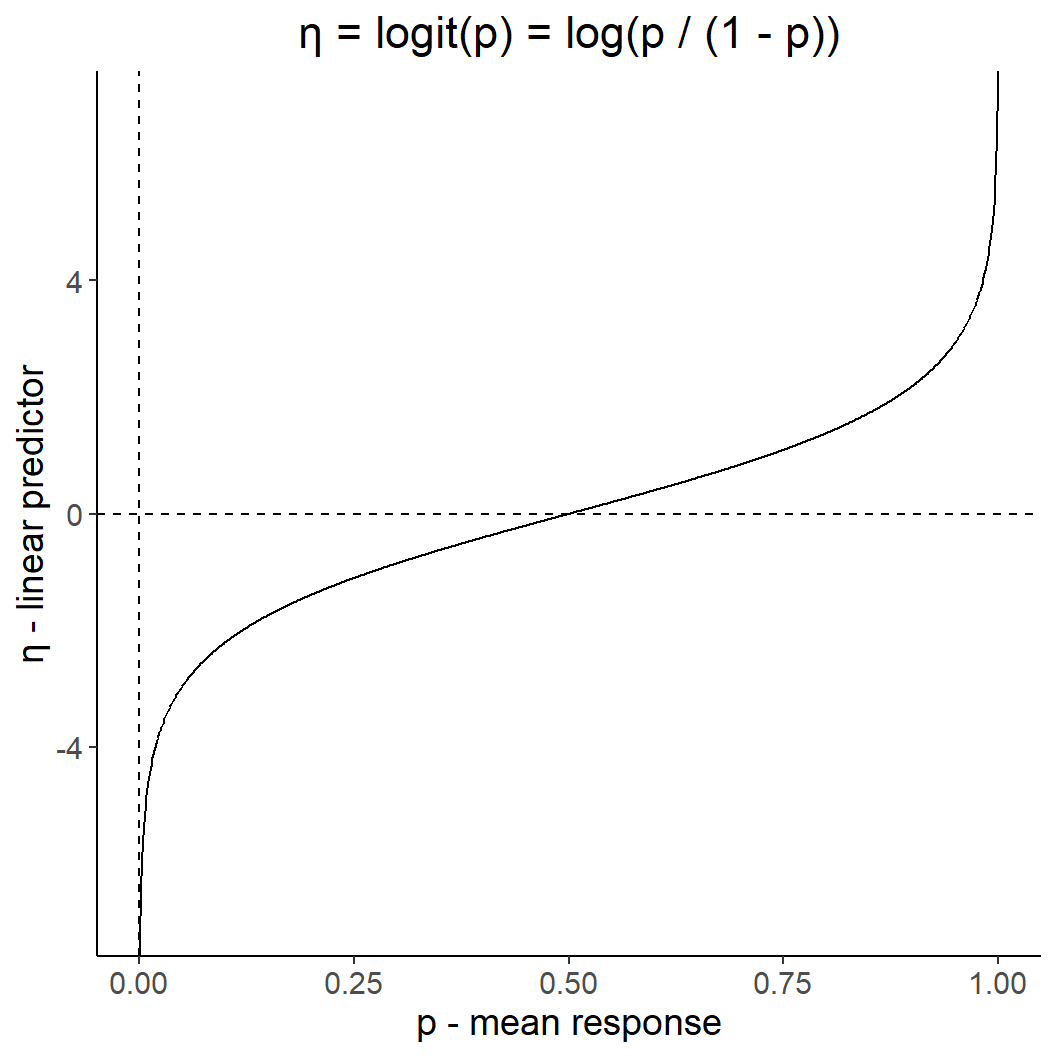
Code
dat <- tibble(y = seq(-5,5, by = 0.01),
p = exp(y)/(1 + exp(y)))
ggplot(dat, aes(y,p)) +
geom_line() +
ggtitle("p = exp(η)/(1 + exp(η))") +
theme(plot.title = element_text(hjust = 0.5)) +
geom_hline(yintercept = 0, linetype = 2) +
geom_vline(xintercept = 0, linetype = 2) +
xlab("η - linear predictor" ) +
ylab("p - mean response")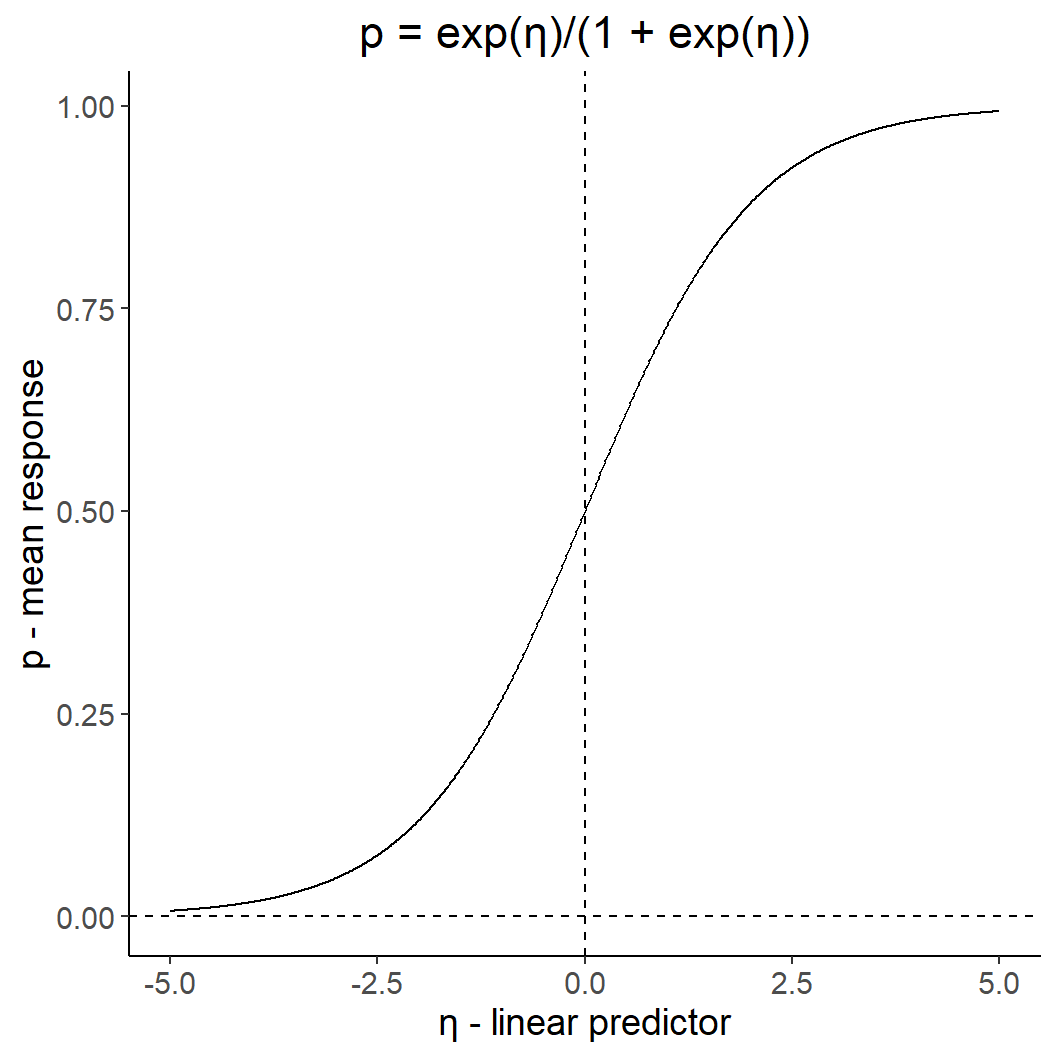
Example: GLM for count data in R
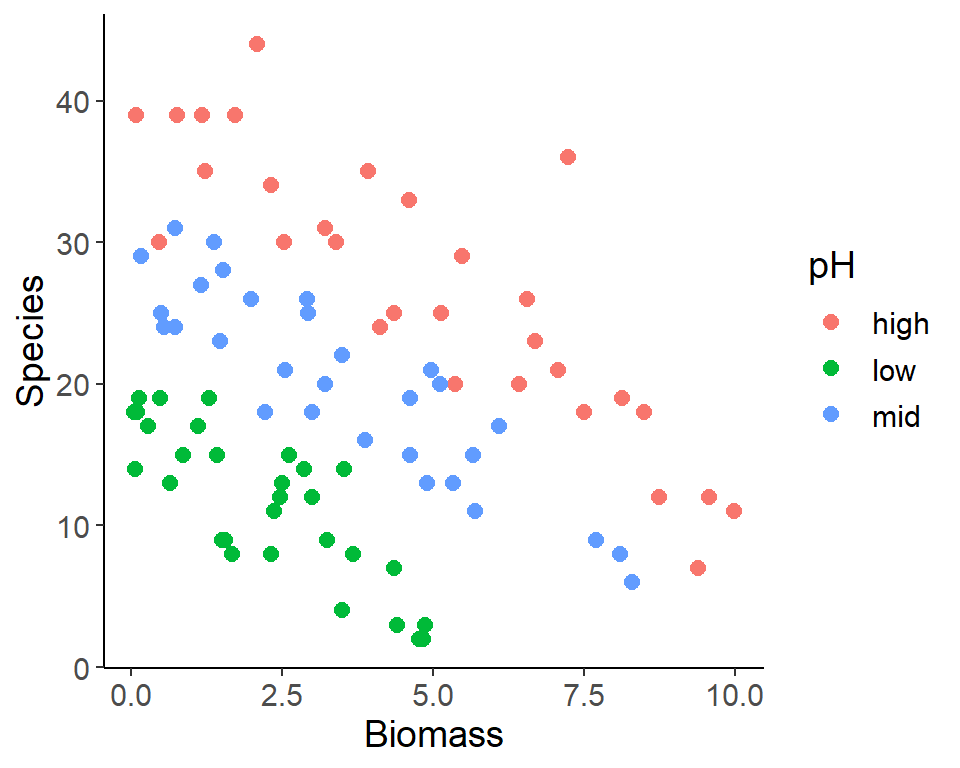
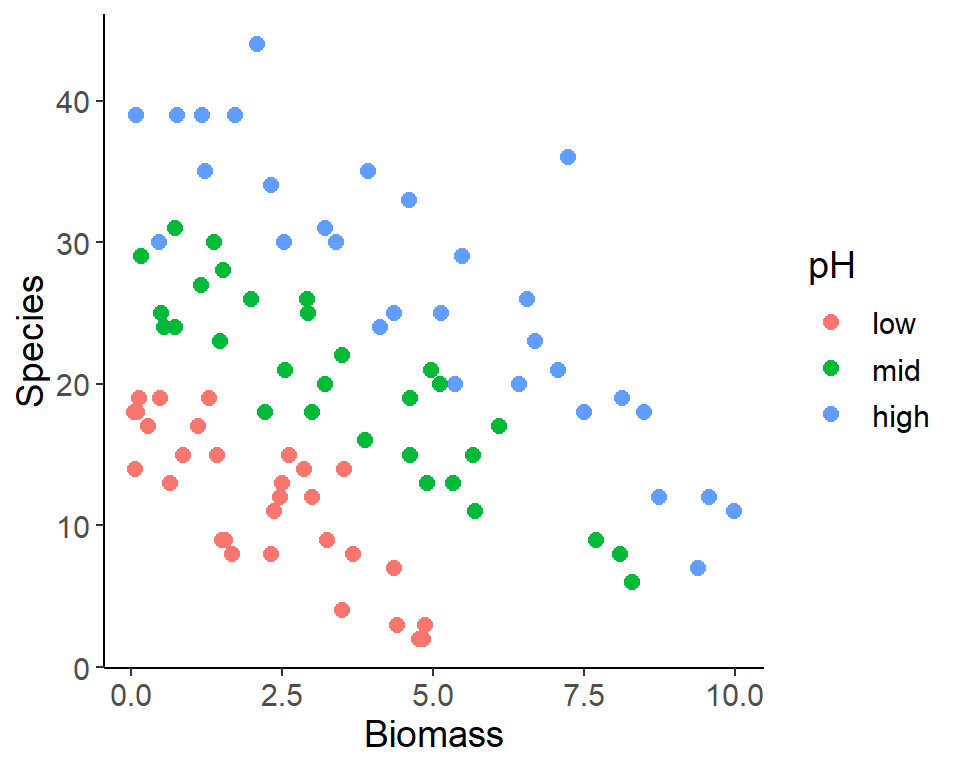
Dataset plant species diversity and biomass
- Response variable:
- No. of plant species in the plot (
Species)
- No. of plant species in the plot (
- Predictor variables:
- Plot biomass (numeric)
- Soil pH (categorical)
Poisson GLM
- Linear predictor: \(\eta_i = \alpha + \sum{\beta_j x_{i,j}}\)
- Inverse link function: \(\lambda_i = exp(\eta_i)\)
- Poisson error distribution \(y_i \sim \mathcal{P}(\lambda_i)\)
Poisson GLM in R
Adjusting factor levels
- Intuitive order of a categorical variable / factor
Fit a GLM in R
glm()function -> similar tolm- Specify error distribution and link function with the
familyargument - Log-link is default with
family = "poisson"
Challenge
- Explain the lines in the coefficients table!
- All values –> scale of link function!
Interpret GLM summary
Call:
glm(formula = Species ~ Biomass * pH, family = "poisson", data = specdat)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.95255 0.08240 35.833 < 2e-16 ***
Biomass -0.26216 0.03803 -6.893 5.47e-12 ***
pHmid 0.48411 0.10723 4.515 6.34e-06 ***
pHhigh 0.81557 0.10284 7.931 2.18e-15 ***
Biomass:pHmid 0.12314 0.04270 2.884 0.003927 **
Biomass:pHhigh 0.15503 0.04003 3.873 0.000108 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 452.346 on 89 degrees of freedom
Residual deviance: 83.201 on 84 degrees of freedom
AIC: 514.39
Number of Fisher Scoring iterations: 4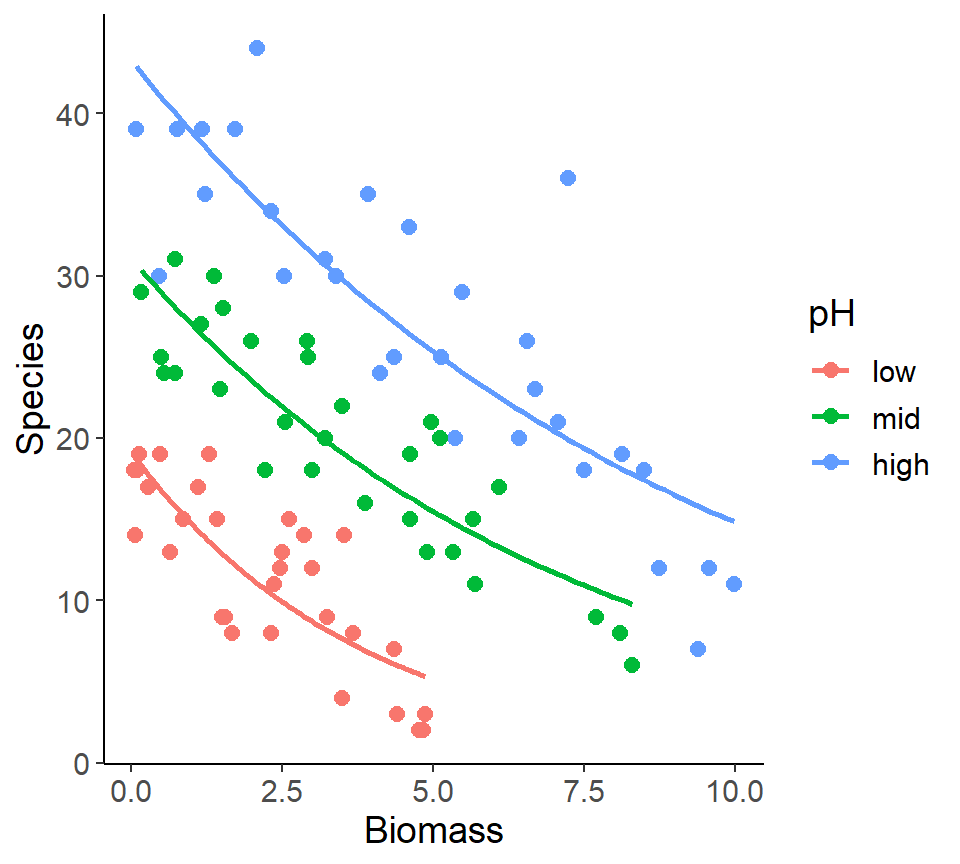
Residual deviance – goodness-of-fit
- Linear models: sum-of-squared errors (SSR) <–> GLMs: residual deviance
- Measure the “goodness-of-fit” in GLMs
- The smaller the (residual) deviance the better the fit
\[\text{Residual Deviance} = -2 \left[ \log\mathcal{L(\text{fitted model})} - \log\mathcal{L(\text{saturated model}}) \right]\]
- \(\log\mathcal{L}\) … log-Likelihood: Probability of the data given the model
- Saturated model: Model which predicts the data perfectly
- Observations = predictions: \(y_i = \mu_i\)
- Null deviance: deviance of a model without explanatory variables
- Higher likelihood of fitted model –> smaller (residual) deviance
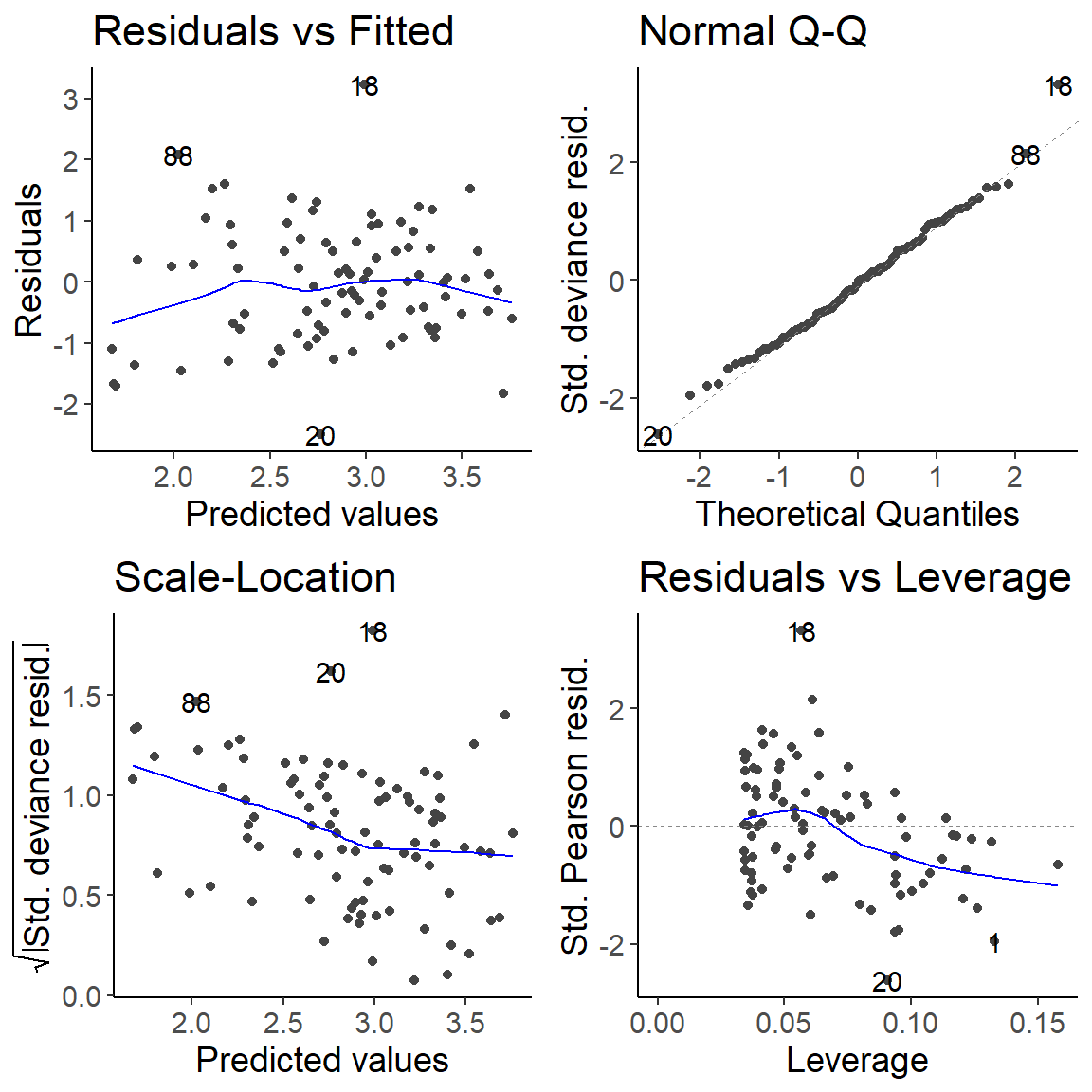
Check model assumptions
Residuals in GLMs
- Raw residuals: observed – predicted; \(r_i = y_i - \mu_i\)
- In GLMs: variance changes with the mean
- Residuals need to be standardized
- By the deviance –> deviance residuals
\[r_i^D = \text{sign}(y_i - \mu_i)\sqrt{d_i}\]
- By the variance –> Pearson residuals
\[r_i^P = \frac{y_i - \mu_i}{\text{sd}(\mu_i)}\]
GLM residuals in R
- Deviance and pearson residuals in
Rresiduals(mod1, type = "deviance")residuals(mod1, type = "pearson")- see
?residuals.glm
Hypothesis test in GLMs
- Likelihood Ratio (LR) = deviance(mod1) - deviance(mod2)
\[ LR = \log\mathcal{L}(mod1) - \log\mathcal{L}(mod2) = \log\left(\frac{\mathcal{L}(mod1)}{\mathcal{L}(mod2)} \right)\]
- Likelihood Ratio Test (LRT)
- LR follows Chi2-distribution
- Degrees of freedom: No. of parameters(mod1) - No. of parameters(mod2)
drop1(mod1, test = "Chi")
Hypothesis tests in GLM
Single term deletions
Model:
Species ~ Biomass * pH
Df Deviance AIC LRT Pr(>Chi)
<none> 83.201 514.39
Biomass:pH 2 99.242 526.43 16.04 0.0003288 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- Residuals deviance of model with interaction in line
<none> - Residual deviance of model without interaction in line
Biomass:pH - Df = 2: Without interaction, only one slope is needed and not 3 (one for each pH level)
- Significant increase in deviance when the interactions is dropped
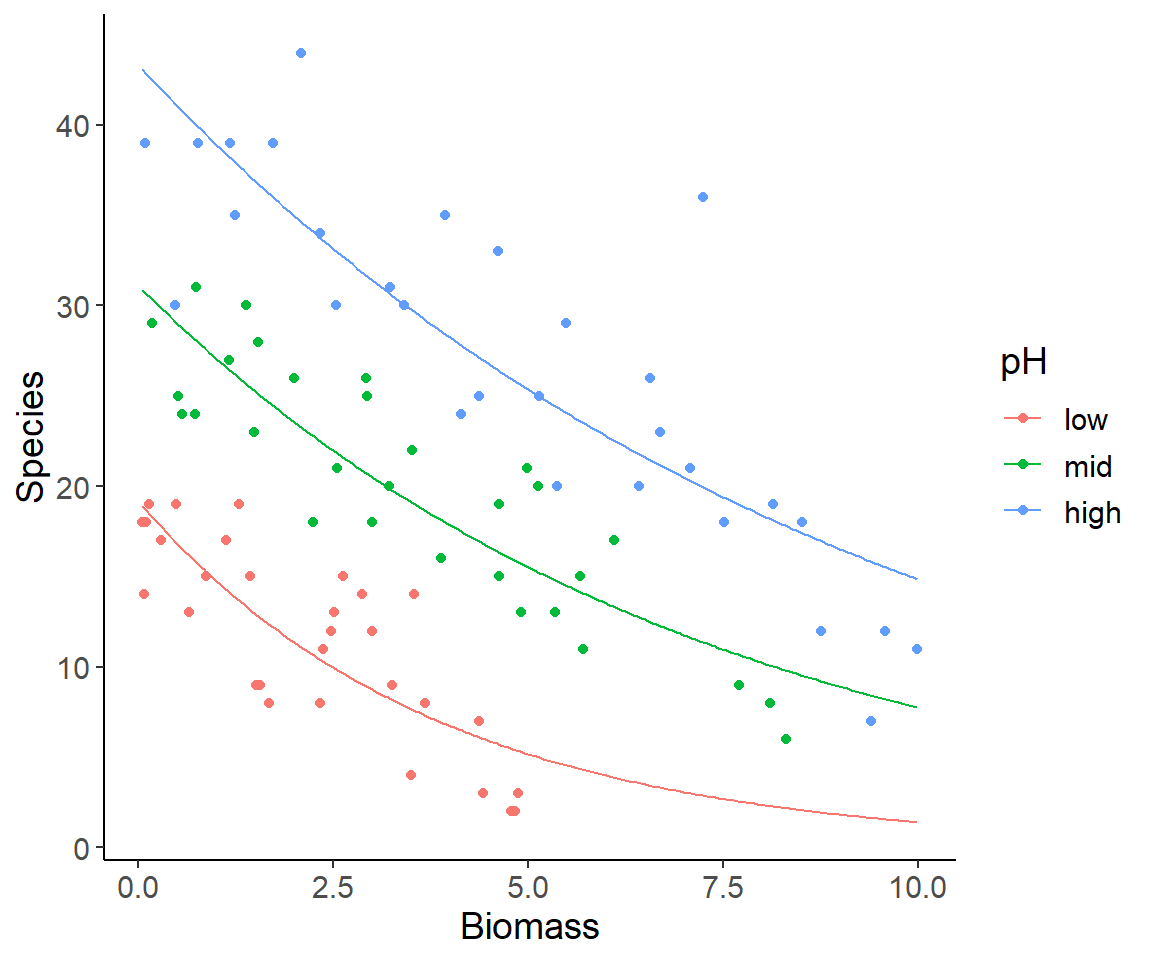
Model predictions
- What does the following code do?
- Create a table with all combinations of an equally-spaced Biomass vector and the values of pH.
Model predictions for GLMs
- Predictions also generated with
predict()
Important
By default predictions for GLMs are on the link function scale.
Use argument type = "response" for predictions on the scale of the response variable!
Plot the predictions
LM vs. GLM
| Linear models | Generalized linear models | |
|---|---|---|
| Model fitting | lm() |
|
| Checking model assumptions | autoplot() |
autoplot() |
| Looking at coefficients | summary() |
summary() |
| Model predictions | predict() |
|
| Hypothesis testing | drop1(..., test = "F") |
drop1(..., test = "Chi") |
Tip
For help on specific function use ?autoplot.lm, ?predict.glm, etc.
Exercises
- Predictions on the link scale
- GLM for binary data
Generalized linear models