Overdispersion in GLMs

Day 8

Felix May

Freie Universität Berlin @ Theoretical Ecology

Reproduce slides

library(tidyr)
library(dplyr)
library(ggplot2)
library(readr)
library(forcats)

## theme for ggplot
theme_set(theme_classic())
theme_update(text = element_text(size = 14))

Overdispersion

  • Poisson GLM

\(\text{mean}(y_i) = \lambda_i\)

\(\text{var}(y_i) = \lambda_i\)

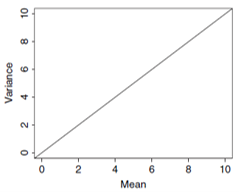
\(\text{var}(y_i) > \lambda_i\)

  • Binomial GLM

\(\text{mean}(y_i) = N_i p_i\)

\(\text{var}(y_i) = N_i p_i (1 - p_i)\)

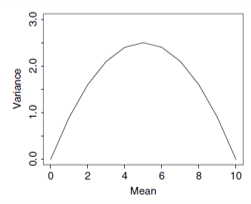
\(\text{var}(y_i) > N_i p_i (1 - p_i)\)

Overdispersion: Higher variance than expected from error distribution

Consequences of overdispersion

Ignoring overdispersion

  • Overestimation of significance, i.e. p-values biased to lower values
    • Inappropriate hypotheses tests
    • Biased predictions
  • Check for overdispersion in Poisson and Binomial-GLMs
    • Not needed for binary data!

Detecting overdispersion

  • Ratio: residual deviance / residual degrees of freedom (df)
  • Residual deviance / df > 1.5 –> overdispersion
  • Residual deviance / df < 0.6 –> underdispersion (rare in the real world)

Model overdispersion

  • Two approaches
  1. Quasi-Likelihood approach
    • Count data –> quasipoisson
    • Proportion data –> quasibinomial
  2. Different error distribution
    • Count data: Negative binomial distribution
      • Extra parameter for the increase in variance relative to Poisson distribution

Quasi-Likelihood approach

  • Assumption: Proportional relationship between \(\text{mean}(y_i)\) and \(\text{var}(y_i)\)
  • Poisson: \(\text{var}(y_i) = \phi \lambda_i\)
  • Binomial: \(\text{var}(y_i) = \phi N_i p_i (1-p_i)\)
  • Estimate \(\phi\) from data \(\phi \approx \frac{\text{Residual deviance}}{\text{df}}\)
  • Consequences
    • Equal parameter estimates than with \(\phi = 1\)
    • Inflation of standard erros by \(\sqrt{\phi}\)

Quasi-Likelihood approach

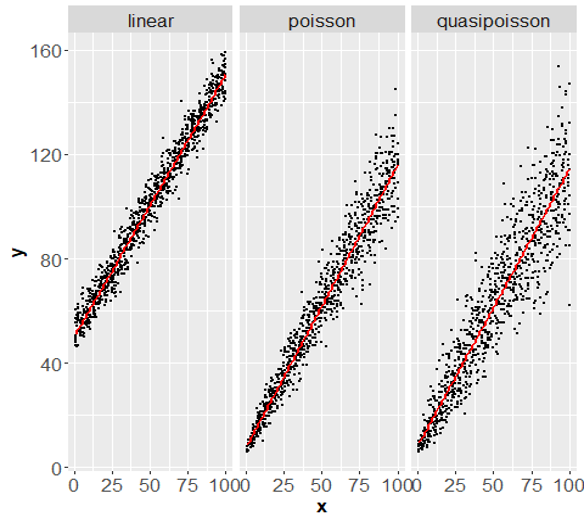
  • Linear regression
    • \(\sigma^2 = c\)
  • Poisson GLM
    • \(\sigma^2 = \lambda\)
  • Quasipoisson GLM
    • \(\sigma^2 = \phi\lambda\)

Negative binomial distribution

  • Discrete distribution for count data
  • Relation to Binomial dist.: No. of failures, until you find a given no. of successes
  • Relation to Poisson dist.: Poisson distribution with variance in \(\lambda\)
  • Different parametrizations in the literature
    • \(\mu\) … mean
    • \(\theta\) .. dispersion parameter
      • Large –> low overdispersion
      • Small –> large overdispersion

\(\text{mean}(y_i) = \mu_i\)

\(\text{var}(y_i) = \mu_i + \frac{\mu_i^2}{\theta}\)

Negative binomial distribution

Code 
x <- 0:25
ypois1 <- dpois(x, lambda = 10)
ynegbinom1 <- dnbinom(x, size = 4, mu = 10)
ynegbinom2 <- dnbinom(x, size = 400, mu = 10)

dat1 <- data.frame(x = rep(x, times = 2),
                   Probability = c(ypois1, ynegbinom1, ypois1, ynegbinom2),
                   Distribution = rep(rep(c("Poisson","Neg. binom"),
                                          each = length(x)), 2),
                   Theta = rep(c(4,400), each = 2*length(x)))

ggplot(dat1, aes(x, Probability, color = Distribution)) +
  geom_point(size = 2) + 
  geom_line(linetype = 2) +
  facet_wrap(~Theta, labeller = label_both)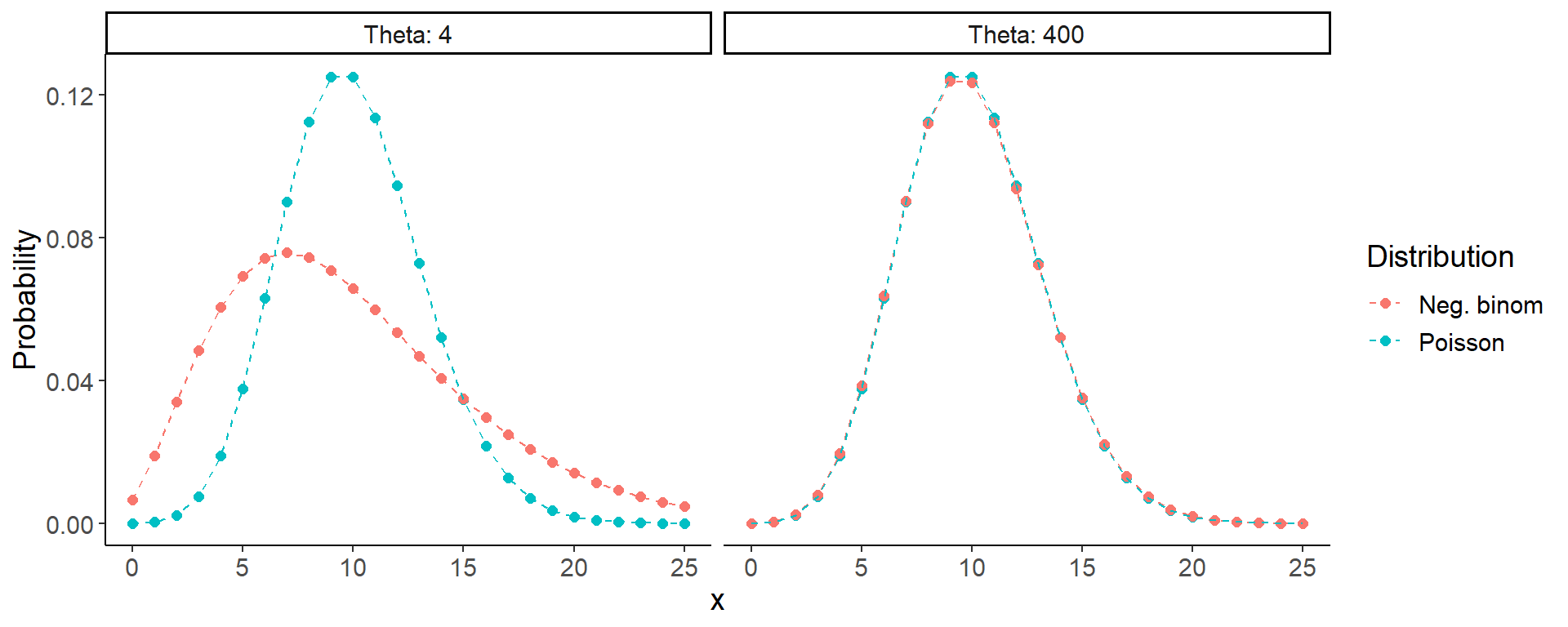

  • \(\mu = 10\) in all panels
  • What are the variances (according to previous slide)?

:::

Insect diversity in urban grasslands

  • Inspired by FU project Flowering campus

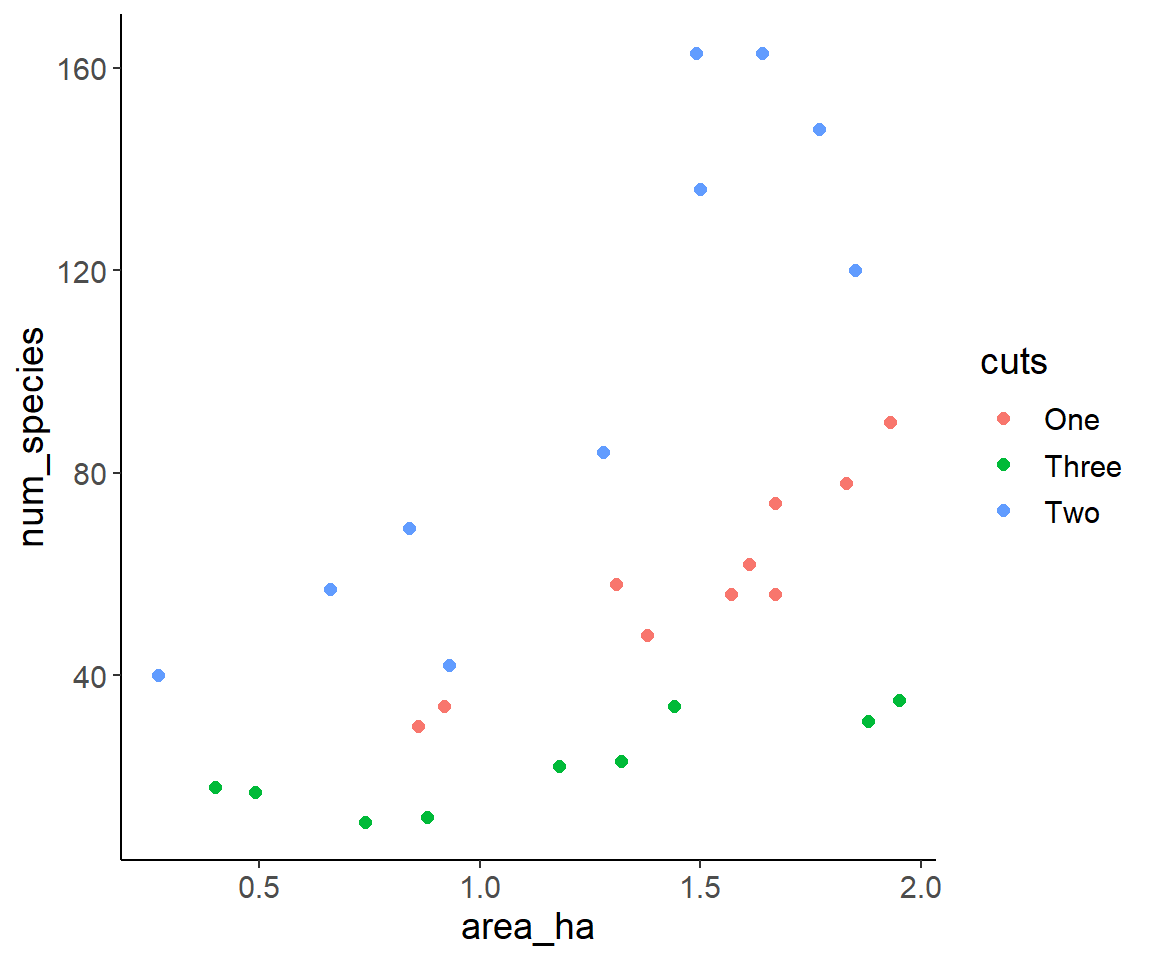
  • Question: How does insect species number vary with mowing frequency and area of the grassland sites?

  • Data set: samples from 30 grassland sites 08_insect_diversity.csv

  • Variables:

    • cuts: number of mowing events per year (consider as categorical variable!)
    • area_ha: area of the grassland site in hectar
    • num_species: total number of insect species over the catching period

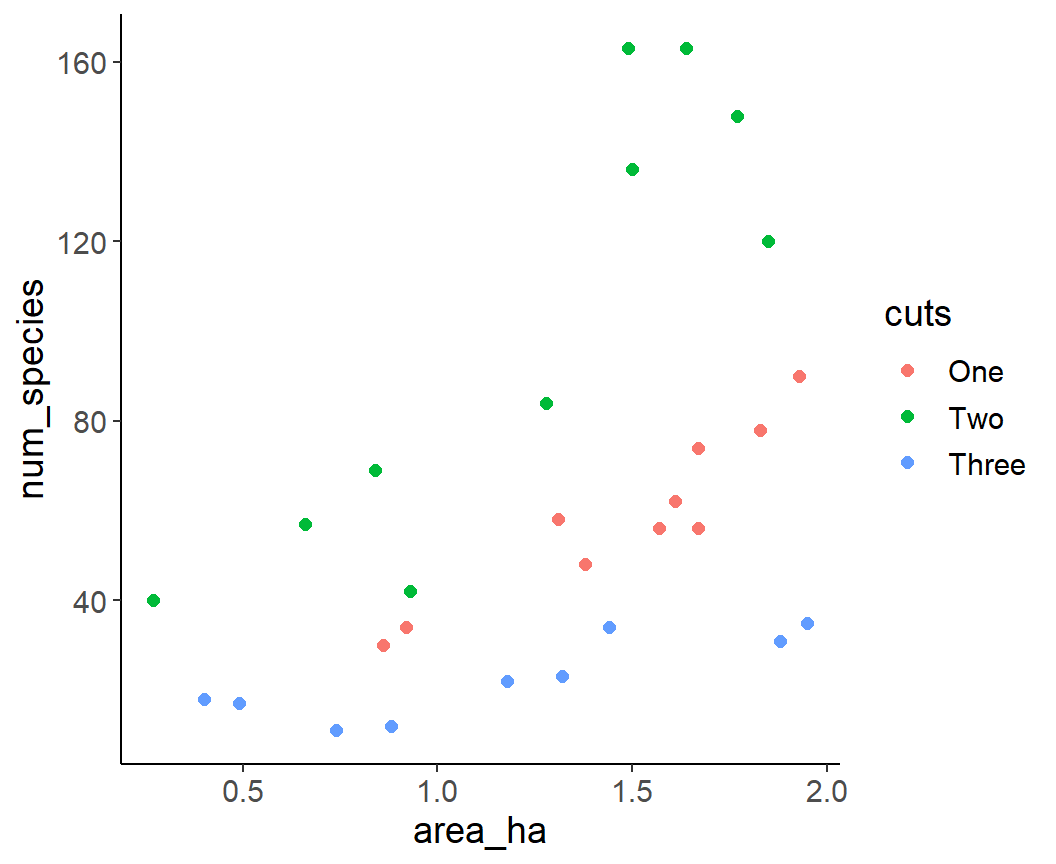
Read and plot

insects1 <- read_csv("data/08_insect_diversity.csv")
insects1
# A tibble: 30 × 3
   cuts  area_ha num_species
   <chr>   <dbl>       <dbl>
 1 One      1.67          74
 2 One      1.38          48
 3 One      1.83          78
 4 One      1.57          56
 5 One      1.61          62
 6 One      0.86          30
 7 One      1.67          56
 8 One      1.31          58
 9 One      1.93          90
10 One      0.92          34
# ℹ 20 more rows
ggplot(insects1, aes(area_ha, num_species, color = cuts )) +
  geom_point(size = 2)

Adjust categorical variable

insects1 <- insects1 %>%
  mutate(cuts = fct_relevel(cuts, "One", "Two", "Three"))
ggplot(insects1, aes(area_ha, num_species, color = cuts )) +
  geom_point(size = 2)

Fit GLM model

  • Test interaction effect between area and no. of cuts naively.
glm1 <- glm(num_species ~ area_ha*cuts, 
            family = "poisson", data = insects1)
drop1(glm1, test = "Chi")
Single term deletions

Model:
num_species ~ area_ha * cuts
             Df Deviance    AIC    LRT Pr(>Chi)  
<none>            66.677 249.65                  
area_ha:cuts  2   71.325 250.30 4.6487  0.09784 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  • Marginally significant interaction with p < 0.1

Check for overdispersion!

summary(glm1)

Call:
glm(formula = num_species ~ area_ha * cuts, family = "poisson", 
    data = insects1)

Coefficients:
                   Estimate Std. Error z value Pr(>|z|)    
(Intercept)        2.653846   0.219913  12.068  < 2e-16 ***
area_ha            0.929122   0.137494   6.758  1.4e-11 ***
cutsTwo            0.752805   0.245878   3.062   0.0022 ** 
cutsThree         -0.276323   0.289262  -0.955   0.3394    
area_ha:cutsTwo   -0.009462   0.156264  -0.061   0.9517    
area_ha:cutsThree -0.330170   0.191993  -1.720   0.0855 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 862.900  on 29  degrees of freedom
Residual deviance:  66.677  on 24  degrees of freedom
AIC: 249.65

Number of Fisher Scoring iterations: 4

Residual deviance / degrees of freedom = 66.7/24 = 2.77 –> Clear overdispersion!

Fit quasi-poisson model in R

glm1a <- glm(num_species ~ area_ha*cuts, 
            family = "quasipoisson", data = insects1)
summary(glm1a)

Call:
glm(formula = num_species ~ area_ha * cuts, family = "quasipoisson", 
    data = insects1)

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)        2.653846   0.362503   7.321 1.46e-07 ***
area_ha            0.929122   0.226646   4.099  0.00041 ***
cutsTwo            0.752805   0.405305   1.857  0.07557 .  
cutsThree         -0.276323   0.476819  -0.580  0.56764    
area_ha:cutsTwo   -0.009462   0.257586  -0.037  0.97100    
area_ha:cutsThree -0.330170   0.316481  -1.043  0.30723    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for quasipoisson family taken to be 2.717213)

    Null deviance: 862.900  on 29  degrees of freedom
Residual deviance:  66.677  on 24  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 4

Tests with Quasi-Likelihood

  • Testing hypothesis in quasi-likelihood models –> F-Test
drop1(glm1a, test = "F")
Single term deletions

Model:
num_species ~ area_ha * cuts
             Df Deviance F value Pr(>F)
<none>            66.677               
area_ha:cuts  2   71.325  0.8367 0.4454
  • Clearly not significant, after accounting for overdispersion!

Negative binomial GLM in R

  • Function glm.nb() from package MASS
library(MASS)
glm1b <- glm.nb(num_species ~ area_ha*cuts, data = insects1)
summary(glm1b)

Call:
glm.nb(formula = num_species ~ area_ha * cuts, data = insects1, 
    init.theta = 53.69134429, link = log)

Coefficients:
                  Estimate Std. Error z value Pr(>|z|)    
(Intercept)        2.66114    0.29494   9.023  < 2e-16 ***
area_ha            0.92437    0.18910   4.888 1.02e-06 ***
cutsTwo            0.70754    0.33672   2.101   0.0356 *  
cutsThree         -0.27814    0.36683  -0.758   0.4483    
area_ha:cutsTwo    0.02343    0.22230   0.105   0.9160    
area_ha:cutsThree -0.32990    0.24785  -1.331   0.1832    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(53.6913) family taken to be 1)

    Null deviance: 402.868  on 29  degrees of freedom
Residual deviance:  26.739  on 24  degrees of freedom
AIC: 232.64

Number of Fisher Scoring iterations: 1

              Theta:  53.7 
          Std. Err.:  24.6 

 2 x log-likelihood:  -218.643

Negative binomial GLM in R

  • Testing hypothesis in negative binomial GLMs –> Likelihood Ratio Test with Chi2-distribution
glm1b <- glm.nb(num_species ~ area_ha*cuts, data = insects1)
drop1(glm1b, test = "Chi")
Single term deletions

Model:
num_species ~ area_ha * cuts
             Df Deviance    AIC    LRT Pr(>Chi)
<none>            26.739 230.64                
area_ha:cuts  2   30.099 230.00 3.3595   0.1864

Overdispersion