Solution to influence of temperature on species growth exercise

1 Load packages

library(readr)
library(dplyr)
library(ggplot2)
library(ggfortify)

## theme for ggplot
theme_set(theme_classic())
theme_update(text = element_text(size = 14))

2 Load data

df_growth <- read_csv("data/05_growth.csv")
df_growth

# A tibble: 100 × 6
   temperature species1 species2 species3 species4 species5
         <dbl>    <dbl>    <dbl>    <dbl>    <dbl>    <dbl>
 1       23.4     5.38     4.87     6.19     7.34     2.92 
 2       11.4     1.85     1.19     1.77     1.91     0.339
 3       19.0     2.65     4.04     5.68     4.11     1.06 
 4       24.8     5.23     5.88     6.25     7.36     7.10 
 5        6.34    0.527    0.463    1.03     0.396    0.096
 6       15.9     3.46     3.15     4.76     3.21     1.01 
 7       14.6     3.00     4.27     1.13     4.95     0.516
 8       22.8     6        4.39     4.45     5.31     4.24 
 9       16.1     3.32     1.36     0.425    3.50     1.31 
10        7.46    0.686    1.09     0.858    0.971    0.32 
# ℹ 90 more rows

2.1 Species 1

lm_species1 <- lm(species1 ~ temperature, data = df_growth)
autoplot(lm_species1, which = 1:2)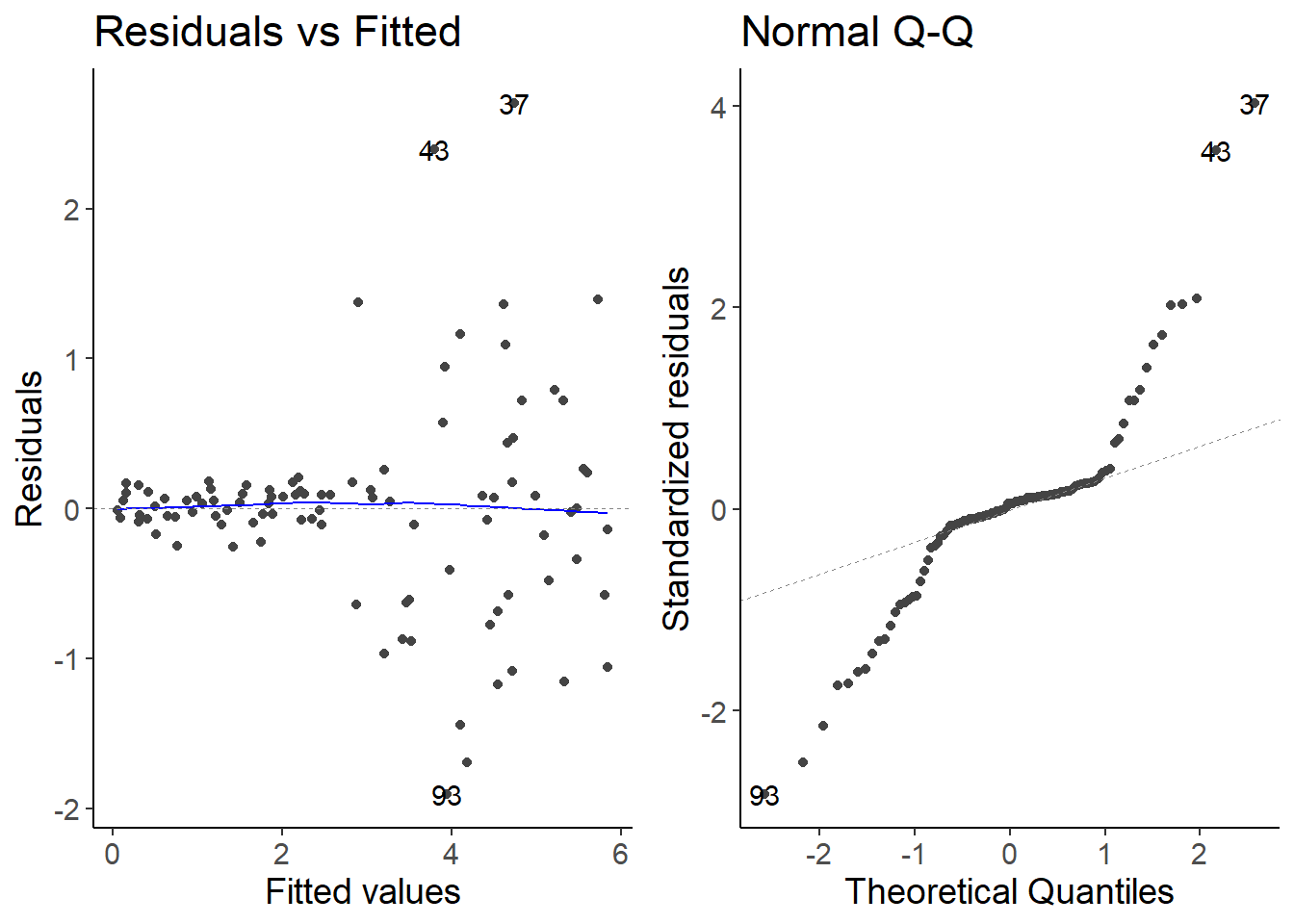

ggplot(df_growth, aes(temperature, species1)) +
    geom_point() +
    geom_abline(intercept = coef(lm_species1)[1],
                slope = coef(lm_species1)[2],
                color = "red", linewidth = 2, 
                alpha = 0.5) + 
    labs(y = "Netto primary production of species 1 [gCm⁻²day⁻¹]",
         x = "Temperature [°C]")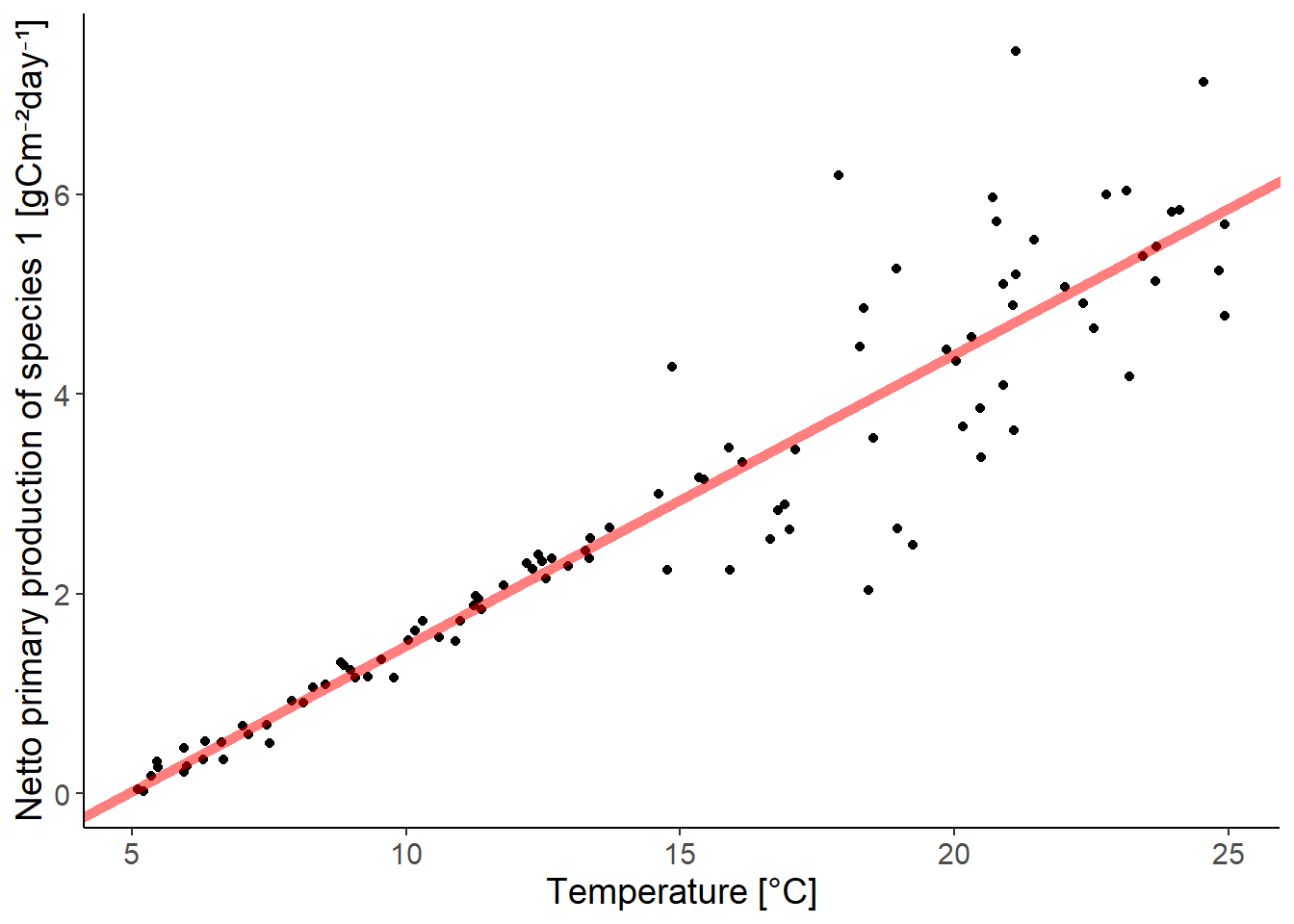 

2.2 Species 2

lm_species2 <- lm(species2 ~ temperature, data = df_growth)
autoplot(lm_species2, which = 1:2)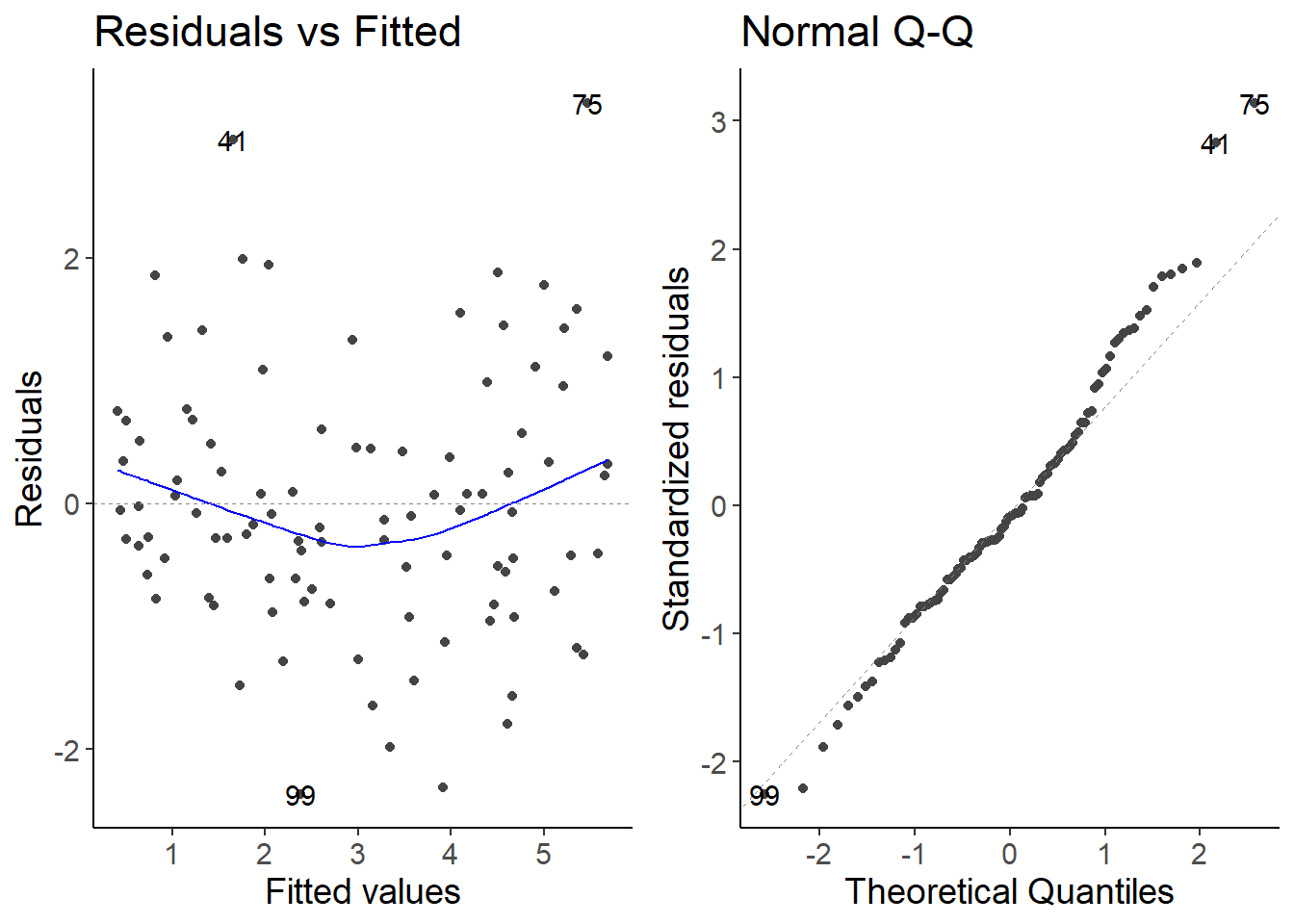

ggplot(df_growth, aes(temperature, species2)) +
    geom_point() +
    geom_abline(intercept = coef(lm_species2)[1],
                slope = coef(lm_species2)[2],
                color = "red", linewidth = 2, 
                alpha = 0.5) + 
    labs(y = "Netto primary production of species 2 [gCm⁻²day⁻¹]",
         x = "Temperature [°C]")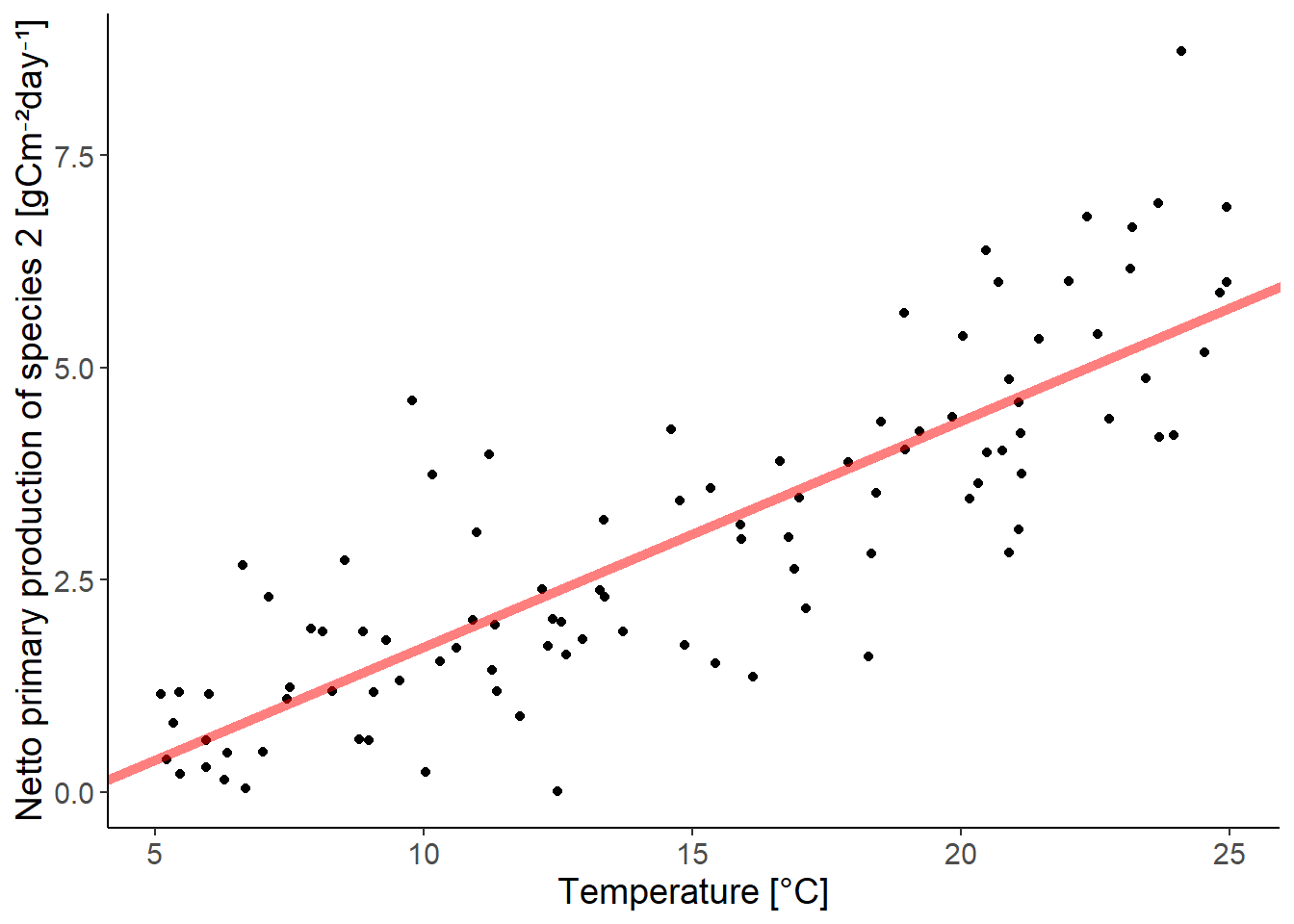 

Everything is fine here, even if there seems to be a slight trend in the residuals.

2.3 Species 3

lm_species3 <- lm(species3 ~ temperature, data = df_growth)
autoplot(lm_species3, which = 1:2)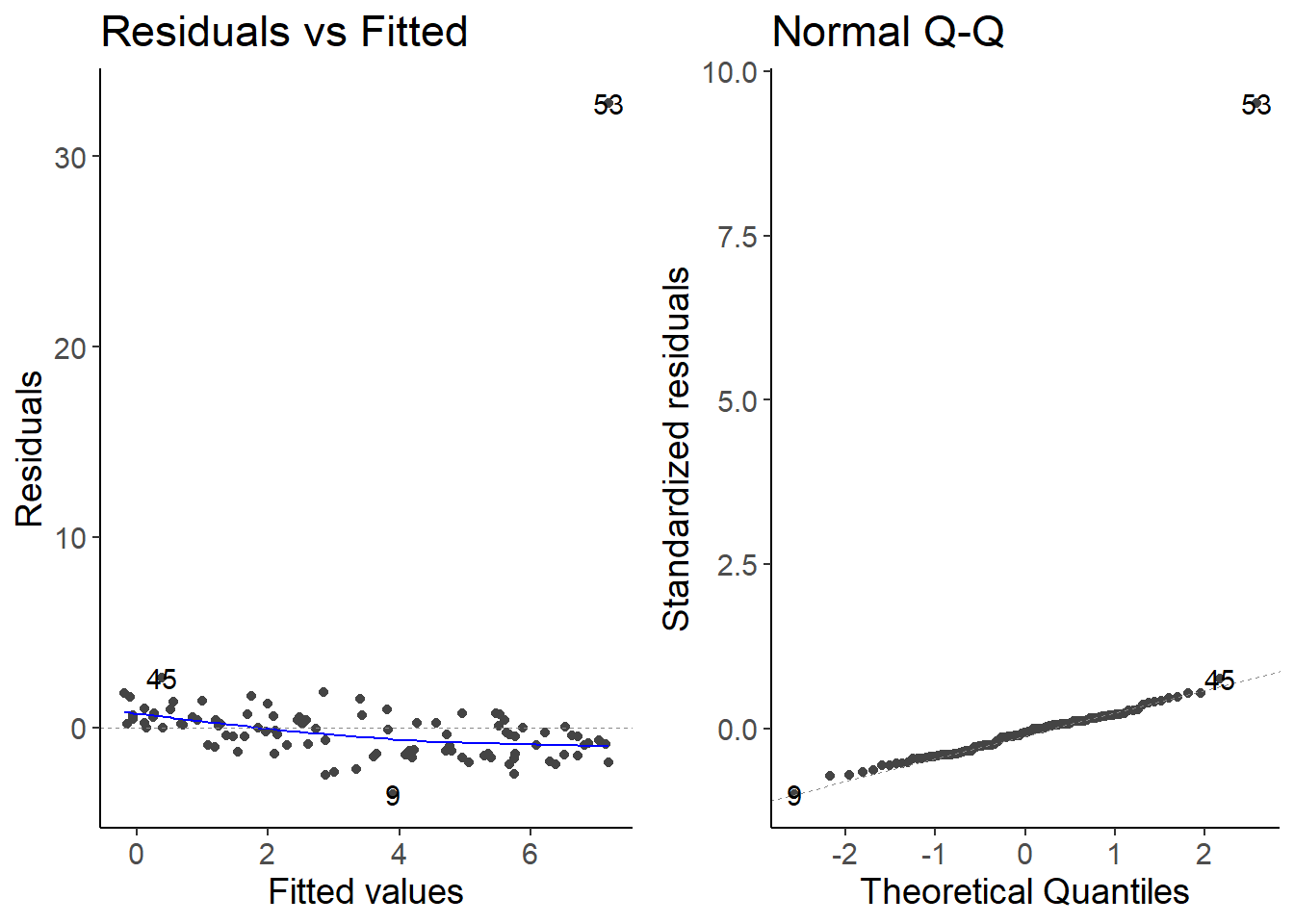

ggplot(df_growth, aes(temperature, species3)) +
    geom_point() +
    geom_abline(intercept = coef(lm_species3)[1],
                slope = coef(lm_species3)[2],
                color = "red", linewidth = 2, 
                alpha = 0.5) + 
    labs(y = "Netto primary production of species 3 [gCm⁻²day⁻¹]",
         x = "Temperature [°C]")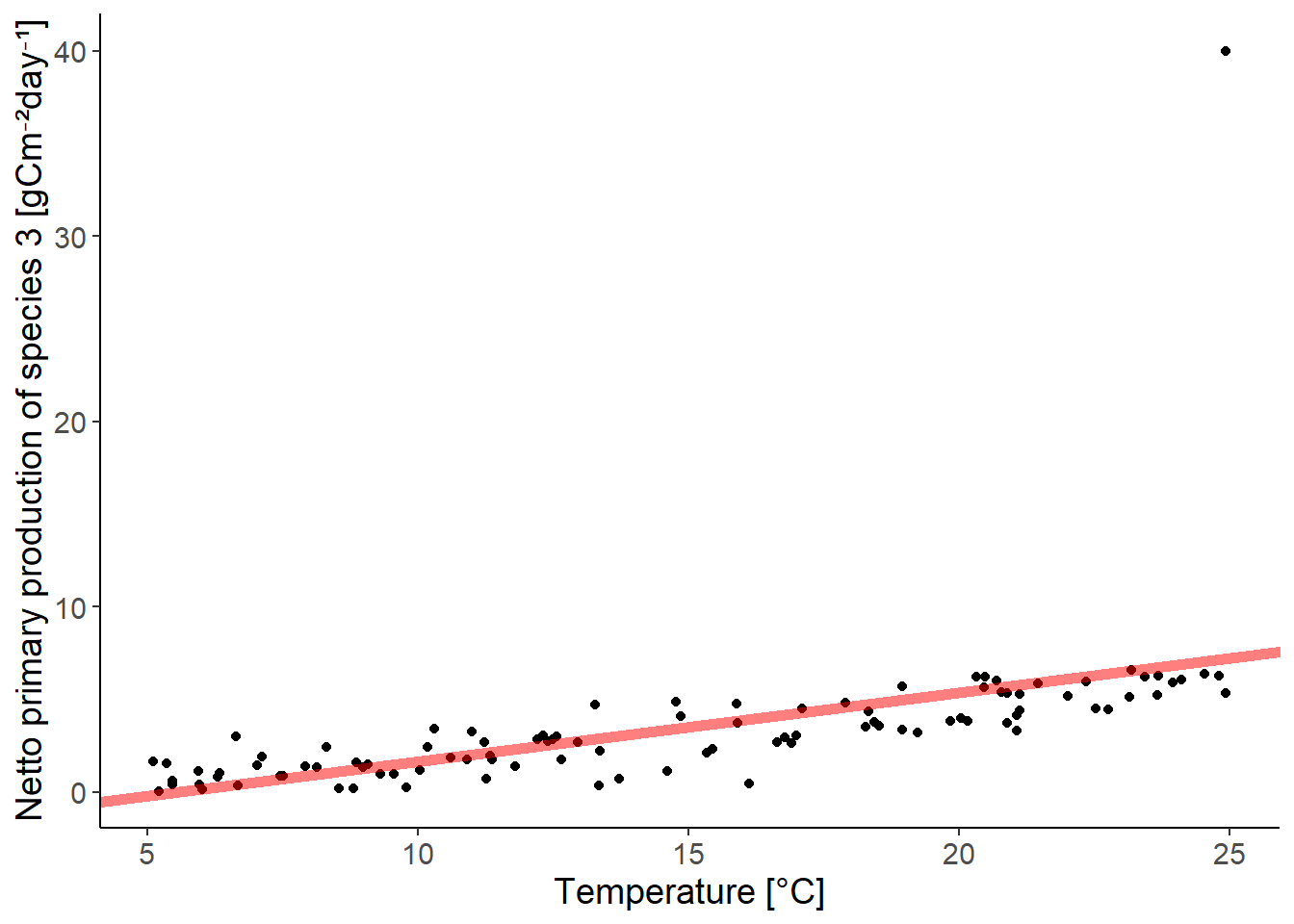 

There is one outlier. You should check if you mistyped the value or if it is a real outlier. If you remove it because you think you made a mistake, you should be transparent about it.

2.4 Species 4

lm_species4 <- lm(species4 ~ temperature, data = df_growth)
autoplot(lm_species4, which = 1:2)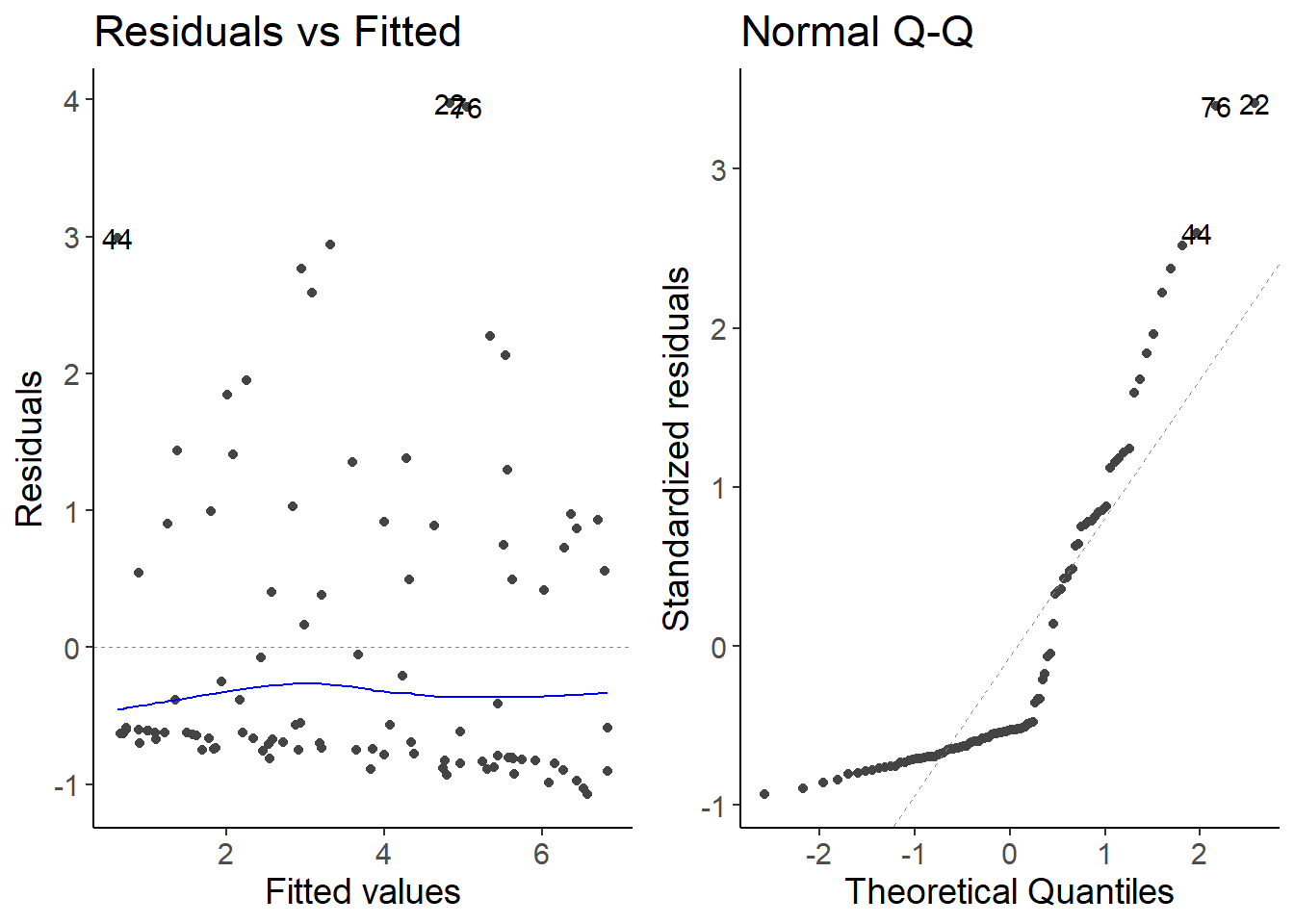

ggplot(df_growth, aes(temperature, species4)) +
    geom_point() +
    geom_abline(intercept = coef(lm_species4)[1],
                slope = coef(lm_species4)[2],
                color = "red", linewidth = 2, 
                alpha = 0.5) + 
    labs(y = "Netto primary production of species 4 [gCm⁻²day⁻¹]",
         x = "Temperature [°C]")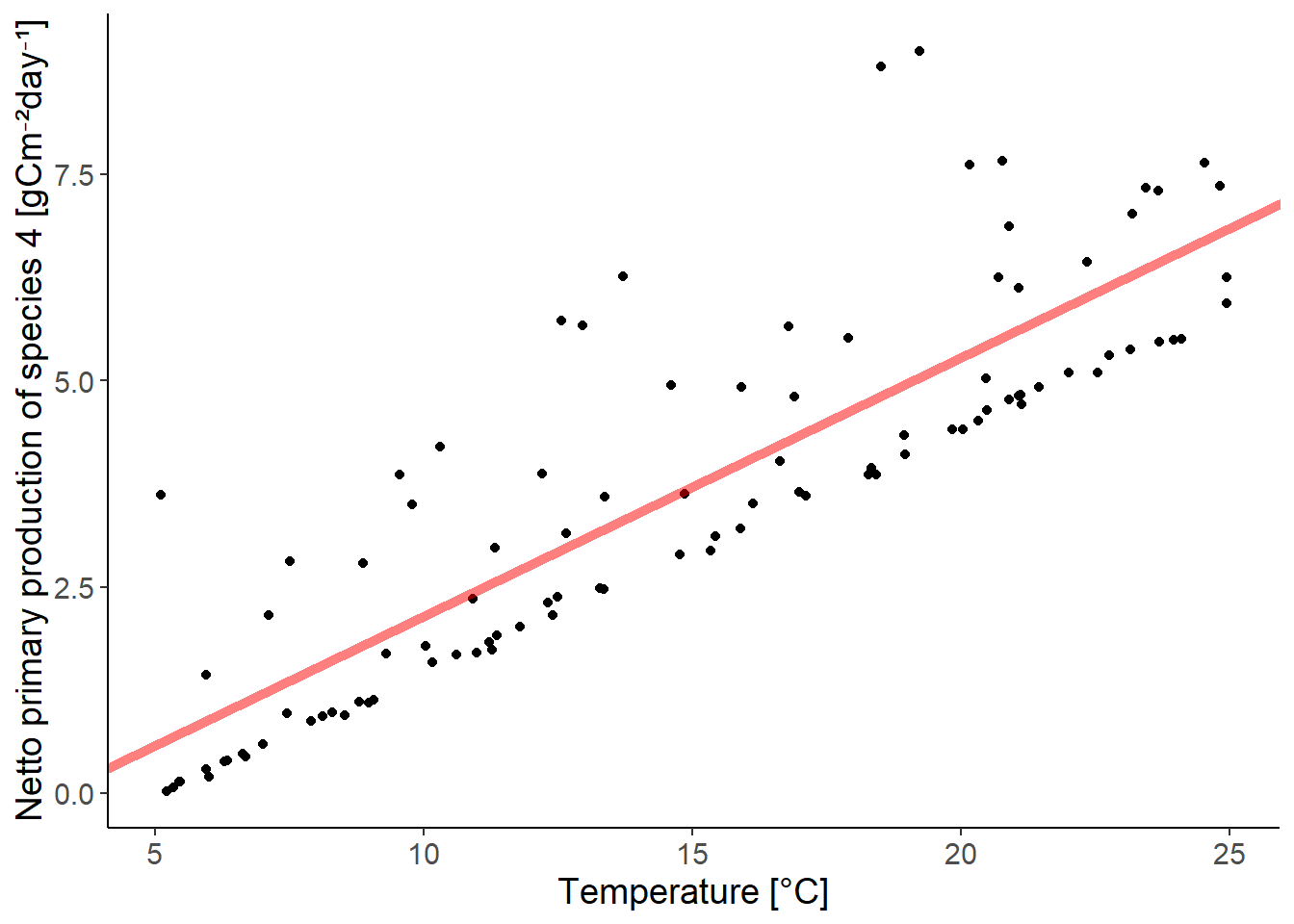 

The residuals do not follow a Normal distribution. The residuals are skewed to the right.

2.5 Species 5

lm_species5 <- lm(species5 ~ temperature, data = df_growth)
autoplot(lm_species5, which = 1:2)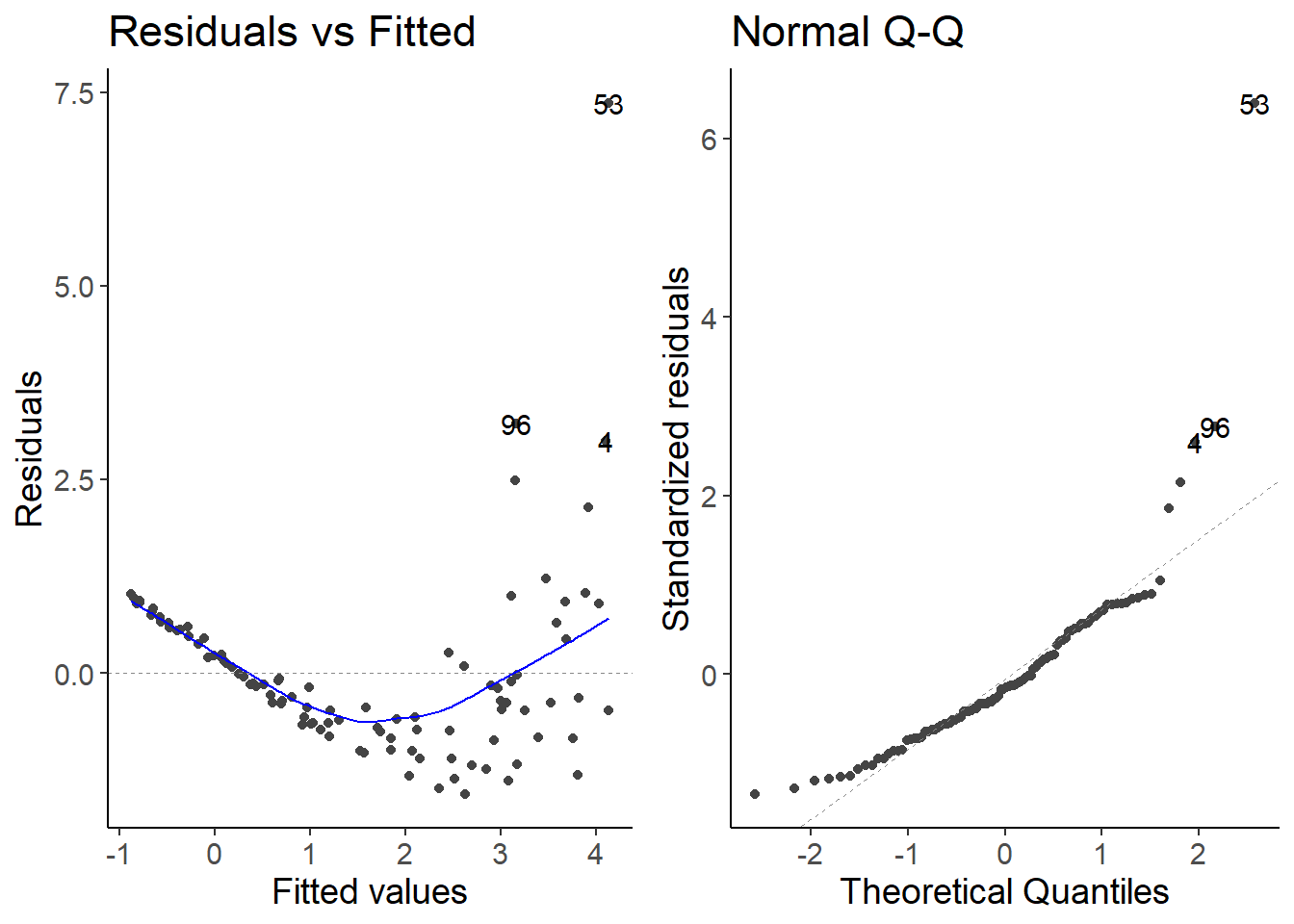

ggplot(df_growth, aes(temperature, species5)) +
    geom_point() +
    geom_abline(intercept = coef(lm_species5)[1],
                slope = coef(lm_species5)[2],
                color = "red", linewidth = 2, 
                alpha = 0.5) + 
    labs(y = "Netto primary production of species 5 [gCm⁻²day⁻¹]",
         x = "Temperature [°C]")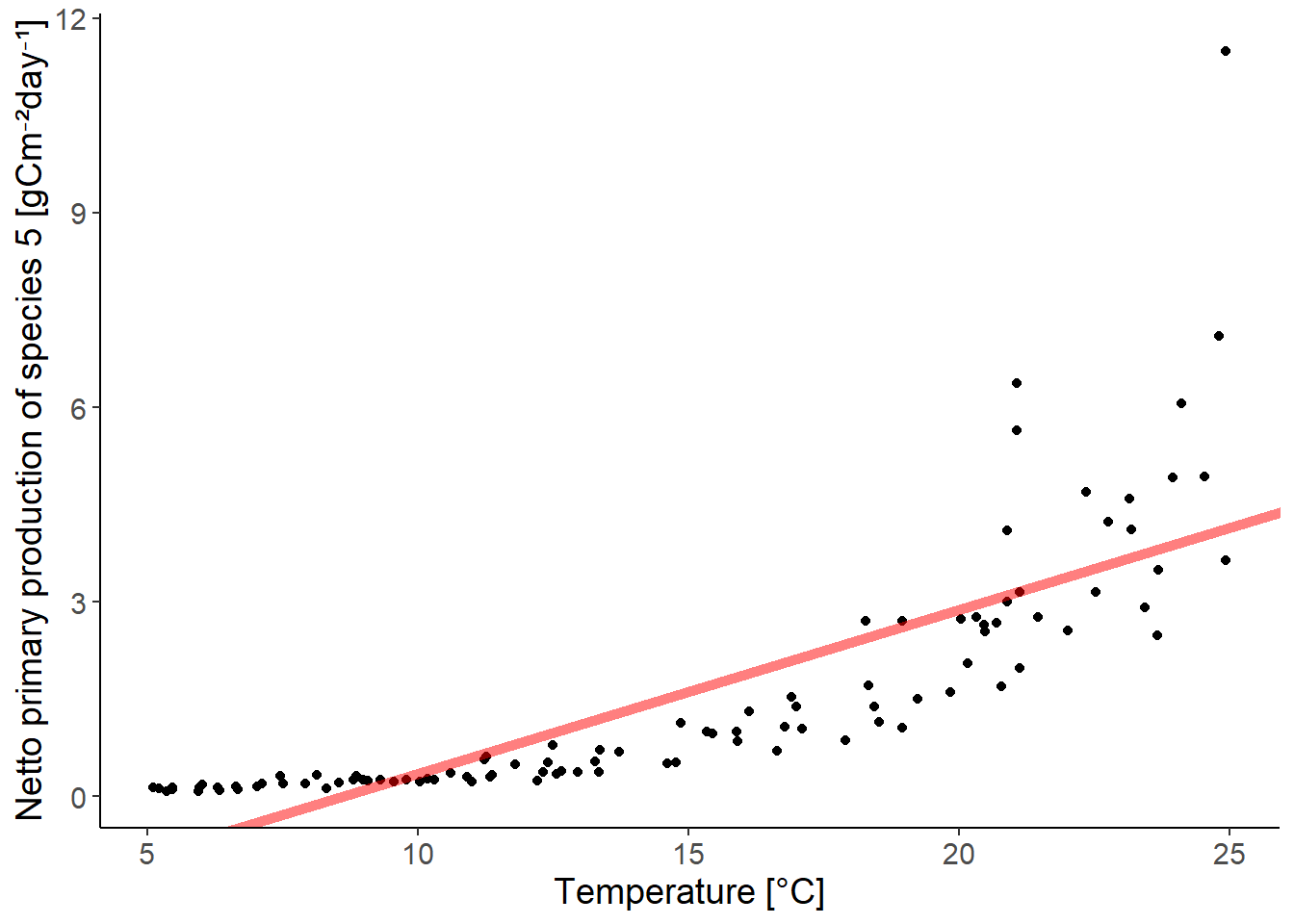 

The relationship between the predictor and the response variable is not linear. There is an exponential relationship. We can transform the response variable to fit an exponential equation.